Large Openings

Theory

The modeling of large openings is a delicate point for semi-open spaces such as train stations. Indeed, in the absence of external wind, there are recirculation phenomena that cause bidirectional flows over the height of the opening.

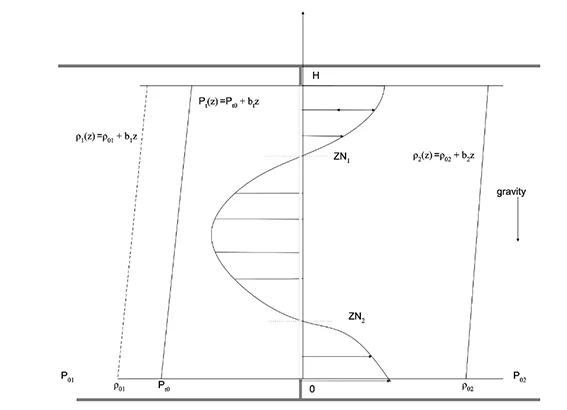
These phenomena are due to differences in pressure and thermal stratification profiles on either side of the flow. In addition, the passage of a free flow through a smaller area causes disturbances on the flow.

In order to model stratified flows without wind effects along large openings, [Feustel, 1998]¹ proposes to use the Bernouilli equation with linear thermal stratification profiles both inside and outside.

$$ \rho_{i} =\rho_{i,0} + b_{i}z $$

In order to be used in a simulation context, i.e. in the absence of measured data, t is therefore necessary to determine these stratification profiles, as well as the tatic pressures at the reference height.

The interior thermal stratification profiles can be deduced from a spatialized aeraulic simulation, and the static pressures are derived from mass balances of a nodal simulation [Allard, 1998]². On the other hand, the outdoor tratification profile and turbulence parameters must be derived from empirical data.

This results in the following velocity profile over the height of the opening:

$$ v_{\text{stack}}(z) = \sqrt{\frac{2}{\rho}\left ( P_{0,\text{ext}}-P_{0,\text{int}}+P_{t0}\right)-\frac{g}{\rho}\left [ \left (\rho_{0,\text{ext}}z+\frac{b_{\text{ext}}z^{2}}{2} \right)-\left (\rho_{0,\text{int}}z+\frac{b_{\text{int}}z^{2}}{2} \right)+b_{t}z\right]} $$

Since the positions of the neutral axes (where the flow changes direction) depend on the velocity we are trying to determine, we can then choose two options:

• Arbitrarily set the height of a single neutral axis at half the height of the opening
• Update the position(s) of the neutral axis(es) (resolution of a second degree equation) according to the speed calculated at the previous time step

Modeling large openings is therefore a challenging problem that requires an exchange of data between an interior spatial model and a nodal model in order to be solved.