Physical properties of aerosols
Kinetic theory of gases
The particles of an aerosol are generally distributed in a gas, e.g. the ambient air. Some of these particles have very small dimensions, such that the shocks with the molecules of the gas transmit their Brownian motion to the particles. Under certain conditions, we can therefore apply the kinetic theory of gases to such small particles.
A environment containing only one type of molecule
Three main hypotheses are accepted:
- The molecules are all identical, spherical and of very low volume \(v_0\) compared to the total volume \(v\) of their whole;
- Their spatial is random and their number remains constant in a given volume;
- The molecules’ movements are uniformly straight and their shocks are elastic.
In these conditions, we can consider a set of molecules in thermal equilibrium. Among these molecules a certain number \(n\) with an excess (or lack) of energy compared to the average thermal activation energy . The molecules of a gas have velocities uniformly distributed in all directions, the quantities of which are themselves distributed according to a probability law called law of Maxwell-Boltzmann . This law represents the probability for a molecule to have its velocity point in the elementary volume \(d\tau = du \cdot dv \cdot dw\).
From these considerations, it becomes possible to determine the number of molecules \(dn\) whose speed is between \(V\) and \(V+dV\).
$$ dn = \frac{n}{2\sqrt{\pi}} \left( \frac{2m}{K_{\text{B}} T} \right)^{3/2} V^2 \exp\left( \frac{m V^2}{2 K_{\text{B}} T} \right) dV $$
Where \(K_{\text{B}} = 1.38064852 \times 10^{-23}\) \([m^2.kg.s^{-2}.K^{-1}]\) is the Boltzmann constant, \(m\) the mass of the molecule and \(T\) the gaz temerature.
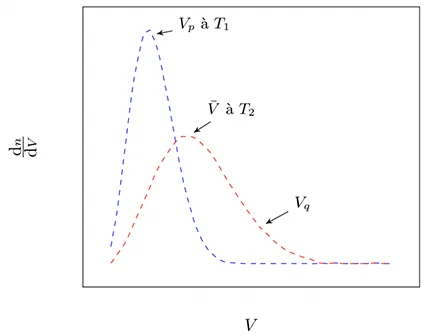
There are three statistical speeds:
- the average speed: \(\bar{V} = \sqrt{\frac{8K_{\text{B}}T}{\pi m}}\),
- the average quadratic velocity: \(V_{\text{q}}=\sqrt{\frac{3K_{\text{B}}T}{ m}}\),
- the most probable speed \(V_{\text{p}}=\sqrt{\frac{2K_{\text{B}}T}{m}}\),
- such that \(V_{\text{p}} < \bar{V} < V_{\text{q}}\).
The particle flow can then be defined \(\varphi=n\frac{\bar{V}}{4}\) as the number of particles passing through a unit surface for a unit of time.
Lastly, during each collision, after rebound, the speed of a molecule changes direction and size. The trajectory of a molecule is therefore a broken line whose different straight portions have different lengths and directions. The length of a segment is the free path of the molecule between two shocks. The arithmetic mean of these free paths is called mean free path \(\lambda_{\text{m}}\) such that:
$$ \lambda_{\text{m}}=\frac{1}{m \pi \sigma^2 \sqrt{2}} $$
\(\sigma\) being the diameter of the molecule. The mean free path is therefore inversely proportional to the concentration.
A environment consisting of two kinds of molecules (or particles)
In the following, we consider an environment closer to the real conditions in which two kinds of molecules or particles \(A\) and \(B\) are present.
The assumptions remain the same as in the previous case. It is further assumed that the two components are in equilibrium, so that the velocity distributions for each of them are Maxwellian.
In this case [Bricard 1977]1 proposes two new expressions for the average free path of each component of the mixture that we will not detail here.
When considering an aerosol \(B\) suspended in a gas consisting of molecule \(A\), the concentration of molecules \(n_A\) and particles \(n_B\) vary from one point to nother. Although the medium under consideration is in thermal and pressure equilibrium, there is a phenomenon of particle transport from the particle-rich regions to the poor regions in such a way that the concentration tends to become uniform in the gas volume. his phenomenon, caused by the thermal agitation of the aerosol components, is referred to as diffusion.
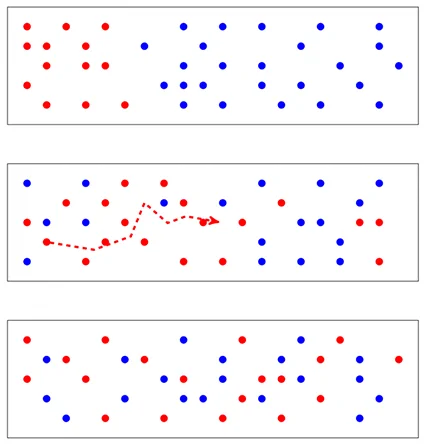
The phenomenon of diffusion (Brownian) is classically modelled using Fick’s two laws . The first law expresses the flow \(\varphi\) of particles moving from areas of high concentration to areas of low concentration while the second law involves time.
$$ \varphi=-D \frac{\text{d}n}{\text{d}z} $$
$$ \frac{\text{d}n}{\text{d}t}=-D \left(\frac{\partial^2 n}{\partial x^2}+\frac{\partial^2 n}{\partial y^2}+\frac{\partial^2 n}{\partial z^2}\right)dt $$
The second law can be modified to take into account external forces communicating a velocity \(V\) to the particle. This results in the Einstein-Fokker’s relationship . The latter approach will be used to take into account the effects of turbulent flows on particles (turbulent scattering).
In order to mark the boundaries between diffusion and convection, a dimensionless number is defined, the number of Péclet:
$$ Pe = \frac{\bar{u} L}{D} $$
We will distinguish between:
- Mutual diffusion: diffusion of the gas-aerosol assembly \((A+B)\) in suspension.
- The diffusion from species \(A\) to species \(B\).
The behaviour of the nucleation mode particles is governed by the Brownian diffusion. The one of the accumulation mode particles is controlled by the turbulent diffusion.
Aerosol sedimentation
Sedimentation is the movement of particles under the action of gravity.
Aerosol particles are subjected to a number of external forces (gravity, electrical forces, aerosol forces, etc.). Depending on the balances acting on a particle, the carrier medium of the aerosol and its particles may no longer be sufficient to compensate for the action of gravity. The particle will then settle on a support at velocity known as the sedimentation rate.
Given the very large variations in linear dimensions and aerosol velocities, the carrier medium can be interpreted as a continuous fluid or a compressible or incompressible corpuscular medium. Several theories have been developed based on the movements of aerosols to determine their sedimentation rate.
The different theories related to aerosol movement [André Renoux 1998]2:
| \(\textrm{Re} \ll 1\) No remote action Laminar flow | \(\textrm{Re} \sim 1\) remote action Turbulence | \(\textrm{Re} > 1\) Mach \(>1\) | |
|---|---|---|---|
| \(r_{\text{p}} \gg \lambda\) | Stokes | Oseen Davies | |
| Continuous medium \(r_{\text{p}} \equiv \lambda\) | Millikan-Cunningham | Krzywobloski-Tsien | |
| Continuous medium \(r_{\text{p}} \ll \lambda\) | Epstein | Tsien | Ashley |
Where:
- \(r_{\text{p}}\) the radius of the aerosol particle,
- \(\lambda_{\text{g}}\) the mean free path of the molecules of the carrier gas,
- \(\textrm{Re}\) the Reynolds number of the particle: \(\textrm{Re}_{\text{p}} =\frac{2 r_{\text{p}} \rho_{\text{g}} V}{\eta}\),
- \(\eta\) the dynamic viscosity of the carrier gas of specific mass ρ\(\rho_{\text{g}}\),
- \(V\) the velocity of the specific mass particle \(\rho_{\text{p}}\),
- \(\bar{u}\) the average speed of the molecules of the carrier gas,
- \(c\) the velocity of sound in the gas,
- \(\frac{V}{c}\) the Mach number.
Stokes’ law
At low Reynolds number (\(\textrm{Re}_{\text{p}} \ll 1\)) the gravitational fall speed of a particle of diameter \(d_{\text{p}}\) in the air is given by the balance between drag according to Stokes’ law and gravity.
The drag force \(F_{\text{d}}\) is such that:
$$ F_{\text{d}} = 3 \pi \nu d_{\text{p}} V $$
The particle’s fall depends on its Archimedes’ thrust \(F_{\text{g}}\) is as:
$$ F_{\text{g}} = g \frac{\pi d^3_{\text{p}} \rho_{\text{f}}}{6} $$
The deposition rate of the particle is then calculated from the balance of the actions acting on the particle:
$$ v_{\text{d}}= \frac{d^2_{\text{p}} g \left(\rho_{\text{p}} - \rho_{\text{f}}\right)}{18 \mu} $$
Velocity Correction Factor - Drag Coefficient \(C_{\text{d}}\)
In turbulent conditions, when the Reynolds number increases, the expression of the drag force becomes:
$$ F_{\text{d}} =C_{\text{d}} \frac{1}{2} A \rho_{\text{f}} v^2_{\text{d}} $$
Where \(C_{\text{d}}\) is a correction coefficient named drag coefficient . We can hen write:
$$ v_{\text{d}}= C_{\text{d}} \frac{d^2_{\text{p}} g \left(\rho_{\text{p}} - \rho_{\text{f}}\right)}{18 \mu} $$
The drag coefficient is defined as the ratio of the drag force to the force of the moving particle. It depends on the Reynolds number.
Velocity correction factor - Cunningham coefficient \(C_{\text{c}}\)
We characterize the continuity of the medium with respect to the radius particle \(r_{\text{p}}\) using the number of Knudsen (dimensionless) \(K_n =\frac{\lambda_{\text{g}}}{r_{\text{p}}}\).
When the particles are smaller in diameter than the mean free path of the molecules of the gas containing them (\(K_n \gg 1\)), the drag force is lower than predicted by tokes’ law because the particles slide on the molecules, as opposed to the continuous regime.
A correction is then made to the drag force using the coefficient of Cunningham calculated from Knudsen’s number:
$$ F_{\text{d}} = \frac{3 \pi \eta d_{\text{p}}}{C_{\text{c}}} $$
Aerosol coagulation
When two particles collide, they may coagulate and form a new larger particle. This phenomenon is also called coalescence. It is all the more important when the number of particles present is high. Generally speaking, it is considered to be influential from 1010 particles per m3. The affected particles are those whose diameter is less than 0.05 µm . Coagulation is an important phenomenon in aerosol physics since it effectively regulates the behaviour, evolution and disappearance of a particulate cloud.
Different coagulation mechanisms exist depending on the size of the particle or the medium in which it is located:
- Brownian movement,
- Collision during flow (laminar or turbulent),
- Sedimentation.
Other physical features
Aerosols are also subject to a number of other physical phenomena involved in the movement of particles. Among others, we will mention:
- Thermophoresis: an aerosol is repelled by a hot body, so that the particles move to areas with low temperatures.
- Photophoresis: the presence or absence of light induces temperature changes that will attract or repel particles.
- Diffusionphoresis: particles suspended in an inhomogeneous gas mixture move under the action of concentration gradients.
- Resuspension: the particles attach themselves to the walls by adhesion under the influence of Van der Walls forces, electrical forces and capillary forces. Some external stresses can lead to the resuspension of particles. However, this phenomenon is difficult to describe given the great influence of the state of the deposition surface (roughness, constituent materials, etc.)