Effet piston en réseau souterrain

Les symboles utilisés dans cette page sont explicités dans une nomenclature située en fin de page.

La connaissance des débits d’air et surpressions en gare souterraine est nécessaire pour évaluer le confort et la sécurité des usagers. Dans le cadre des travaux menés sur la qualité d’air en gare souterraine , on cherche notamment à estimer l’ordre de grandeur de la quantité d’air déplacée au niveau des quais de station suite à l’arrivée et au départ d’un train.

Notion de pertes de charge

Lorsqu’un fluide est en mouvement dans un conduit, une partie de son énergie est dissipée par frottement correspondant à une perte de charge. Deux types de perte de charge peuvent être considérés :

Les pertes de charges linéaires. La différence de pressions induite par ces pertes de charge peut s’exprimer par le biais de la formule de Darcy suivante :

$$ \Delta P =\frac{\rho\lambda Lv^2}{2D_{\text{h}}} $$

Où $P$ est la pression, $v$ est la vitesse de l’air, $L$ est la longueur du conduit, $D_{\text{h}}$ est le diamètre hydraulique et $\lambda$ un coefficient de perte de charge linéaire.

Les pertes de charges singulières que l’on modélise par le biais d’un coefficient $\xi$ pouvant être estimé par exemple en se servant d’abaques tables d’Idelchik ¹.

La différence de pressions occasionnée au passage d’une singularité peut s’écrire comme :

$$ \Delta P_\text{tot} =\frac{\rho v^2}{2 }\left(\frac{ \lambda L }{D_{\text{h}}}+\xi\right) $$

Mise en équation du phénomène

Le calcul de l’effet piston dans une gare souterraine demande de modéliser un réseau de galeries dans lesquelles un train va se déplacer suivant un trajet linéaire et marquant un certain nombre d’arrêts. Il s’agit donc de représenter des écoulements transitoires en 1D, pilotés par la différence de pression induite par le mouvement du train.

réseau aeraulique souterrin — *Exemple de réseau souterrain (logiciel SPES1D-AREP)*

Les équations permettant d’établir ce modèle simplifié s’appuie sur les principes de conservation de la masse et de la quantité de mouvement (rappelées ici ) à partir desquelles il est possible de calculer la vitesse de l’air mis en mouvement par le train.

Pour cela, il est nécessaire d’appliquer le théorème de Bernouilli généralisé à un volume de contrôle de fluide environnant le train.

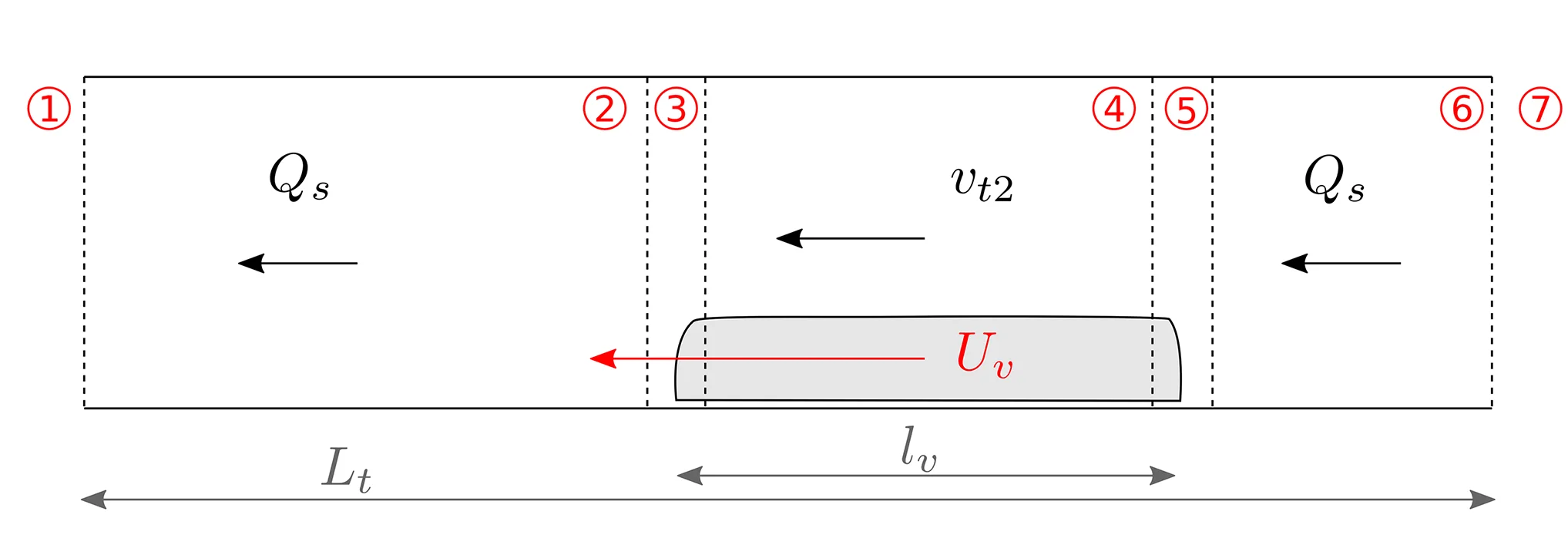
effet piston souterrain — *Schéma illustrant l’effet piston*

On aboutit alors à l’équation gouvernant l’évolution du débit d’air dans un tunnel:

$$ \rho C \frac{\mathrm{d}Q_{\text{s}}}{\mathrm{d}t} = \underbrace{\Delta P_{\text{sing}} + \Delta P_{\text{lin}} + \Delta P_{\text{fan}} + \Delta P_{\text{piston}} }_{w(Q_{\text{s}})}+\Delta P_{\text{ext}} $$

Où $\Delta P_\text{sing}$ correspond à la différence de pression générée au niveau d’une singularité, $\Delta P_\text{lin}$ correspond à la différence de pressions induite par frottement dans une section constante, $\Delta P_\text{fan}$ correspond à la différence de pressions due à la ventilation mécanique, $\Delta P_\text{piston}$ correspond à la différence de pressions causée par l’effet piston dû au mouvement du train et $\Delta P_\text{ext}$ est la différence de pression entre les deux extrémités du segment de conduit étudié.

$C$ est le terme inertiel de la colonne d’air :

En absence de train : $C=\frac{L_{\text{t}}}{A_{\text{t}}}$
En présence de train : $C=\frac{L_{\text{t}}-l_{\text{v}}}{A_{\text{t}}}+\frac{l_{\text{v}}}{A_{\text{t}}-a_{\text{v}}}$

En notant $L_{\text{t}}$ la longueur du segment de tunnel, $l_{\text{v}}$ celle du véhicule dans le segment, $A_{\text{t}}$ la section du segment de tunnel et $a_{\text{v}}$ celle du véhicule dans le segment.

La littérature fournit des expressions de ces différents $\Delta P$ synthétisées dans la table suivante:

	Sans Train	Avec Train
$\Delta P_\text{lin}$	$-\frac{\rho f_t L_{\text{t}} P_t \mid Q_{\text{S}} \mid Q_{\text{S}}}{8 A_{\text{t}}^3}$	$ -\frac{\rho f_t L_{\text{t}} P_t \mid Q_{\text{S}} \mid Q_{\text{S}}}{8 A_{\text{t}}^3} $
$\Delta P_\text{sing}$	$-k\rho\frac{\mid Q_{\text{S}} \mid Q_{\text{S}}}{2 A_{\text{t}}^2}$	$-k\rho\frac{\mid Q_{\text{S}} \mid Q_{\text{S}}}{2 A_{\text{t}}^2}$
$\Delta P_\text{fan}$	$\rho\frac{ \mid Q_\text{fan}\mid \left(v_{\text{fan}}-\frac{Q_{\text{S}}}{A_{\text{t}}}\right)}{A_{\text{t}}}$	$\rho\frac{ \mid Q_\text{fan} \mid \left(v_\text{fan}-\frac{Q_{\text{S}}}{A_{\text{t}}}\right)}{A_{\text{t}}}$
$\Delta P_\text{piston}$	$0$	$\frac{\rho (\textcolor{limegreen}{K_{vB}}+\textcolor{red}{K_{vF}})(A_{\text{t}} U_{\text{v}}-Q_{\text{S}})^2}{2 A_{\text{t}}^2} + \frac{\rho f_t l_{\text{v}} P_t \mid (a_{\text{v}} U_{\text{v}}-Q_{\text{S}})\mid (a_{\text{v}} U_{\text{v}}-Q_{\text{S}})}{8 (A_{\text{t}}-a_{\text{v}})^3}+\frac{\rho \lambda_{\text{v}} l_{\text{v}} P_v \mid (a_{\text{t}} U_{\text{v}}-Q_{\text{S}})\mid (a_{\text{t}} U_{\text{v}}-Q_{\text{S}}) }{8 (A_{\text{t}}-a_{\text{v}})^3}+\frac{\rho a_{\text{v}} l_{\text{v}}}{A_{\text{t}}-a_{\text{v}}}\frac{dU_{\text{v}}}{dt} \textcolor{limegreen}{+\rho \frac{Q_{\text{S}}^2}{2 A_{\text{t}}^2}-\rho\frac{(a_{\text{v}} U_{\text{v}}-Q_{\text{S}})^2}{2 (A_{\text{t}}-a_{\text{v}})^2}}\textcolor{red}{-\rho\frac{Q_{\text{S}}^2}{2 A_{\text{t}}^2}+\rho\frac{(a_{\text{v}} U_{\text{v}}-Q_{\text{S}})^2}{2 (A_{\text{t}}-a_{\text{v}})^2}}+\frac{\rho f_t l_{\text{v}} P_t \mid Q_{\text{S}}\mid Q_{\text{S}}}{8 A_{\text{t}}^3}$

Les termes en rouges doivent être pris en compte lorsque l’avant du train est présent dans le segment étudié. Les termes en vert doivent être introduits lorsque l’arrière du train présent dans le-dit segment.

Note :
En régime permanent et en l’absence de train, l’équation régissant l’effet piston peut être ramenée à l’équation suivante :
$$ \Delta P = Z Q_{\text{s}}^2 $$

Cette équation est communément utilisée pour l’étude de réseaux hydrauliques avec la méthode des $Z$ mais compte tenu de l’importance des effets transitoires générés par le passage du train, celle-ci n’est pas applicable dans ce contexte.

Résolution du réseau

Les équations du phénomène étant désormais écrites pour tous les segments constituant le réseau, il convient de réordonner celles-ci afin d’aboutir à un système d’équations de la forme :

$$ \rho\left[\underline{\underline{C}}\right]\cdot\left[\underline{\dot{Q_{\text{s}}}}\right]=\left[\underline{\omega}(Q_{\text{s}})\right] $$

Pour cela, nous utilisons les méthodes des nœuds et des mailles (similaires à celles utilisées en génie électrique) illustrées ci-dessous:

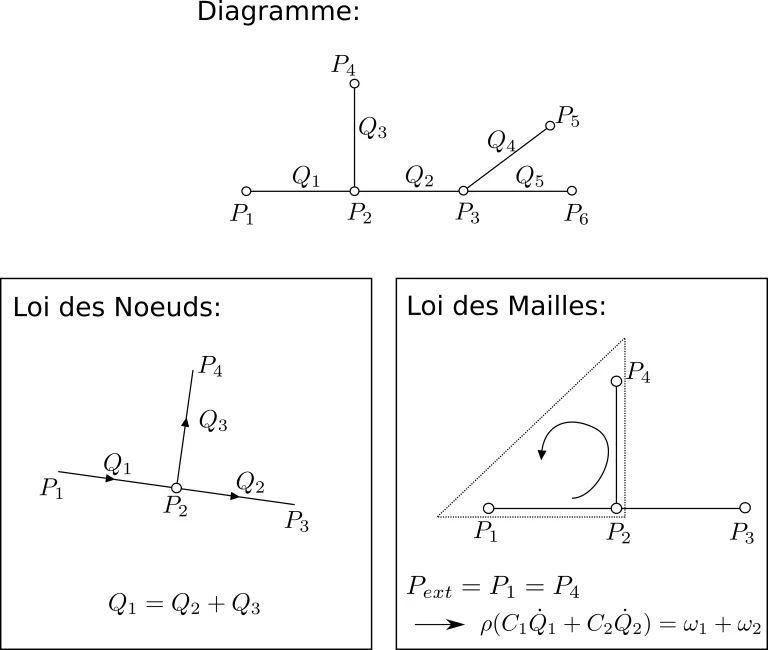
diagramme maille noeud resolution — *Diagramme des noeuds et mailles*

Le système transitoire peut alors être résolu en utilisant un schéma de résolution explicite .

Présentation du logiciel SPES1D

Le logiciel SPES1D (pour Subway Piston Effect Simulation in 1D) a été développé par nos équipes pour résoudre le problème transitoire du train circulant dans des tunnels et gares souterraines.

Ce logiciel introduit trois catégories de segments pour couvrir un vaste ensemble de cas:

l’élément de type conduit. Cet élément est le plus basique. Il peut être utilisé autant tant pour les tunnels, les gares (si le train ne s’arrêtent pas) que les conduits divers (jonctions entre deux bâtiments voyageurs, passages souterrains,…).
l’élément de type gare. Cet élément est utilisé pour marquer un arrêt. L’arrêt est tel que le centre de l’élément est confondu avec le centre du train lorsque la vitesse de ce dernier est nulle.
l’élément de type conduit avec ventilation. Cet élément permet de tenir compte des effets d’une ventilation mécanique.

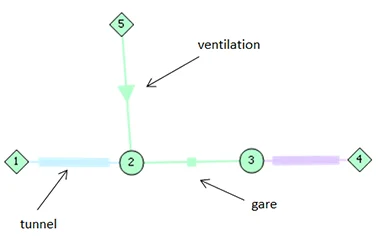
SPES elements — *Éléments proposés dans SPES1D*

Il est alors possible de déterminer l’évolution de l’ensemble des variables du réseau au cours du trajet du train.

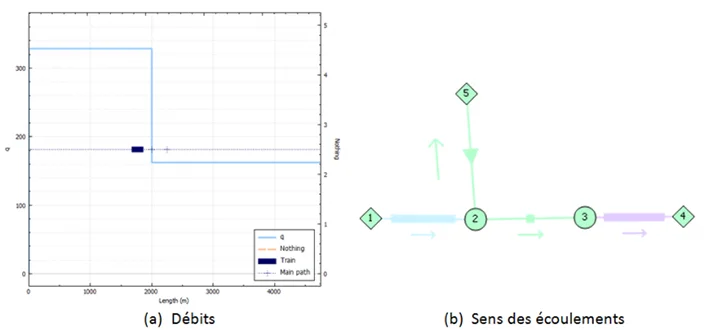
debit aeraulique train entree gare — *Débit sur le trajet du train à l’entrée en gare et sens des écoulements associés*

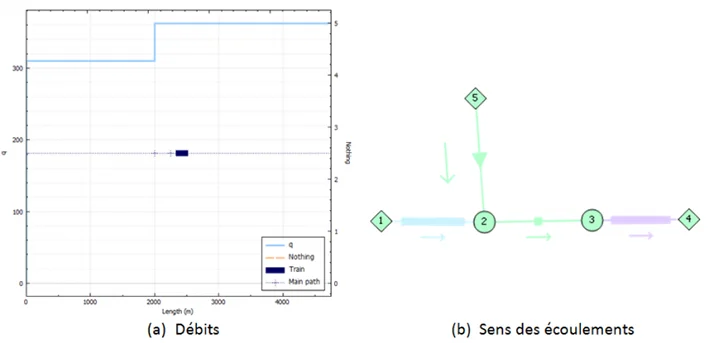
debit aeraulique train sortie gare — *Débit sur le trajet du train en sortie en gare et sens des écoulements associés*

Validation

Le logiciel développé SPES1D a été validé après comparaison avec l’étude de [Sajben, 1971] ². Dans son article, Sajben étudie l’effet piston d’un train placé dans un segment et dont la puissance propulsive est constante. Il observe notamment que dans la configuration étudiée et en régime établi, lorsque le train atteint 21 m/s, l’air dans le tunnel est déplacé de 8,2 m/s. La même configuration a été modélisée avec notre logiciel SPES1D. Il en résulte qu’en régime établi et pour un train circulant à 21 m/s, la vitesse de l’air déplacé est galement de 8,2 m/s.

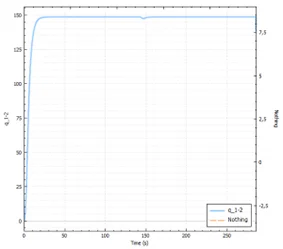
Nomenclature

Symbole	Signification
$A$	Aire [m²]
$A_{\text{t}}$	Aire du tunnel [m²]
$a_{\text{v}}$	Aire du véhicule [m²]
$C$	Terme inertiel de la colonne d’air
$D_{\text{h}}$	Diamètre hydraulique [m]
$K_{\text{vb}}$	Coefficient de perte de charge brusque dûe à l’expansion de l’air suite au passage du train
$K_{\text{vf}}$	Coefficient de perte de charge brusque dûe à la contraction de l’air au passage du train
$P$	Pression [Pa]
$\Delta P_{\text{ext}}$	Différence de pressions entre les extrémités du segment [Pa]
$\Delta P_{\text{sing}}$	Variation de pressions au sein d’une singularité [Pa]
$\Delta P_{\text{lin}}$	Différence de pressions dûe aux frottements [Pa]
$\Delta P_{\text{fan}}$	Différence de pressions induite par la ventilation mécanique [Pa]
$\Delta P_{\text{piston}}$	Différence de pressions induite par effet piston [Pa]
$f_t$	Coefficient de perte de charge régulière au niveau du tunnel
$L$	Longueur [m]
$L_{\text{t}}$	Longueur du tunnel [m]
$l_{\text{v}}$	Longueur du train [m]
$\lambda$	Coefficient de perte de charge régulière
$\lambda_{\text{v}}$	Coefficient de perte de charge régulière au niveau du train
$Q$	Débit [kg/m³]
$Q_{\text{s}}$	Débit d’air ventilé par effet piston [kg/m³]
$U_{\text{v}}$	Vitesse du train [m/s]
$v$	Vitesse de l’air [m/s]
$\rho$	Densité de l’air [kg/m³]
$Z$	Résistance hydraulique
$\xi$	Coefficients de perte de charge singulière

Idelchik, I. E., 1986, Handbook of hydraulic resistance. Washington. Lien PDF ↩︎
Sajben, M. (1971). Fluid Mechanics of Train-Tunnel Svstems in Unsteady Motion. AIAA Journal, 9(8), 1538-1545. DOI ↩︎