Grandes ouvertures

Théorie

La modélisation des grandes ouvertures est un point délicat pour les espaces semi-ouverts tels que les gares. En effet, en l’absence de vent, il existe toutefois des phénomènes de recirculation qui causent des écoulements bidirectionnels sur la hauteur de l’ouvrant.

Ces phénomènes sont dus aux différences de pression, et de profils de stratification thermique de part et d’autre de l’écoulement. De plus, le passage d’un écoulement libre à travers une zone plus restreinte engendre des perturbations sur l’écoulement.

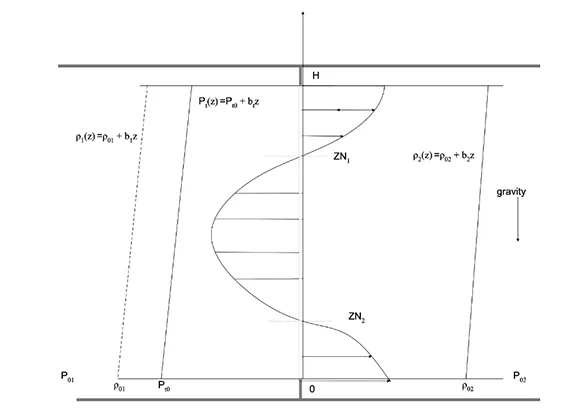
Afin de modéliser les écoulements stratifiés sans effets du vent le long des grandes ouvertures, [Feustel, 1998]¹ propose d’utiliser l’équation de Bernouilli avec des profils de stratification thermiques linéaires à l’intérieur comme à l’extérieur.

$$ \rho_{i} =\rho_{i,0} + b_{i}z $$

Afin d’être utilisée dans un contexte de simulations, c’est-à-dire en l’absence de données mesurées, il faut donc déterminer ces profils de stratification, ainsi que les pressions statiques au niveau de référence.

Les profils de stratification thermiques côté intérieur peuvent être déduits d’une simulation aéraulique spatialisée, et les pressions statiques sont issues des bilans massiques d’une simulation nodale [Allard, 1998]². En revanche, le profil de stratification extérieur et les paramètres de turbulence doivent provenir de données empiriques.

On obtient donc le profil de vitesse suivant sur la hauteur de l’ouvrant :

$$ v_{\text{stack}}(z) = \sqrt{\frac{2}{\rho}\left ( P_{0,\text{ext}}-P_{0,\text{int}}+P_{t0}\right)-\frac{g}{\rho}\left [ \left (\rho_{0,\text{ext}}z+\frac{b_{\text{ext}}z^{2}}{2} \right)-\left (\rho_{0,\text{int}}z+\frac{b_{\text{int}}z^{2}}{2} \right)+b_{t}z\right]} $$

Étant donné que les positions des axes neutres (où l’écoulement change de sens) dépendent de la vitesse que l’on cherche à déterminer, on peut alors choisir deux options :

• Fixer arbitrairement la hauteur d’un unique axe neutre à la moitié de la hauteur de l’ouvrant,
• Mettre à jour la ou les positions des axes neutres (résolution d’une équation du second degré) en fonction de la vitesse calculée au pas de temps précédent.

La modélisation des grandes ouvertures est donc un problème épineux qui requiert un échange de données entre un modèle spatialisé intérieur et un modèle nodal afin d’être résolu.