Méthode des $Z$

Il est souvent utile d’avoir recours à des approches simplifiées pour le calcul des débits et pressions dans un réseau plutôt que de mettre en œuvre un calcul de mécanique des fluides lourd, complexe et coûteux. On présente ici la méthode dite des $Z$, ou méthode des impédances hydrauliques (par analogie électrique) pour le calcul des débits de fluide dans un système de nœuds et branches. Les pressions y tiennent le rôle du potentiel tandis que les débits représentent l’intensité.

Equation gouvernante

Entre deux points d’un écoulement, l’équation de Bernoulli régissant la perte de charge linéaire, liée au coefficient de friction linéaire $\lambda$, ainsi que singulière (facteur $\xi$) est la suivante :

$$ \Delta p = \frac{\rho v^2}{2} \times \Big (\frac{\lambda L}{D_{\text{h}}} + \xi \Big ) \text{ [Pa]} $$

Pour l’exprimer en fonction du débit $Q_{\text{v}}$ dans une conduite de section $S$ il vient :

$$ v^2 = \frac{2}{\rho} \Delta p \times \Big (\frac{\lambda L}{D_{\text{h}}} + \xi \Big )^{-1} \text{ [m²/s²]} $$

$$ Q_{\text{v}}^2 = \frac{2 S^2}{\rho (\frac{\lambda L}{D_{\text{h}}} + \xi)} \Delta p $$

L’expression suivante du débit apparaît alors :

$$ Q_{\text{v}} = S\sqrt{\frac{2}{\rho(\frac{\lambda L}{D_{\text{h}}} + \xi)} } \sqrt{\Delta p} \text{ [m3/s]} $$

La méthode dite des $Z$ consiste à exprimer la perte de charge sous la forme $\Delta p = Z \times Q_{\text{v}}^2$, qui ressemble fort à la loi d’Ohm . Dans le cas présent cela équivaut à :

$$ \Delta p = \frac{\rho(\frac{\lambda L}{D_{\text{h}}} + \xi)}{2S^2} \times Q_{\text{v}}^2 \text{ [Pa]} $$

Soit alors la “résistance hydraulique” (ou aéraulique) $Z$ :

$$ Z = \frac{\rho}{2S^2} \Big (\frac{\lambda L}{D_{\text{h}}} + \xi \Big ) \text{ [Pa.s²/m}^6\text{]} $$

Intégration du coefficient de décharge $C_{\text{d}}$

Une grandeur fréquemment utilisée en aéraulique est le coefficient de décharge $C_{\text{d}}$ qui donne la réduction de débit occasionnée au passage d’un orifice du fait de la constriction du jet, notamment par effets inertiels, et des frottements visqueux. On notera que la valeur de ce coefficient est sujette à caution – voir la section dédiée .

Si l’on souhaite convertir le coefficient de décharge d’un ouvrant en perte de charge, il faut revenir à la définition du problème et calculer la résistance aéraulique $Z$ équivalente à partir de l’équation liant $Q_{\text{v}}$ et $C_{\text{d}}$ :

$$ Q_{\text{v}} = C_{\text{d}} S \sqrt{ \frac{2 \Delta p}{\rho}} $$

Afin de pouvoir écrire “l’égalité du flux” sous une forme permettant le calcul de la résistance aéraulique équivalente on transforme l’équation précédente en :

$$ Q_{\text{v}}^2 = \frac{2 (C_{\text{d}} S)^2 }{\rho}\Delta p $$

Ceci nous donne un $Z$ équivalent tel que :

$$ Z = \frac{\rho}{2 (C_{\text{d}} S)^2 } $$

Pour des résistances aérauliques en série il suffira d’additionner les $Z$ de chaque élément. Par exemple, le $Z$ équivalent combinant pertes de charge linéique et singulière ($\lambda, \xi$) ainsi que la réduction du débit liée à un coefficient de décharge $C_{\text{d}}$ d’un ouvrant, vaut :

$$ Z_\text{eq} = \frac{\rho}{2S^2} \Big (\frac{\lambda L}{D_{\text{h}}} + \xi + \frac{1}{C_{\text{d}}^2} \Big ) $$

Nous sommes donc en mesure de mettre en équation un système régissant l’équilibre des pressions et débits : il s’agit de le poser et de résoudre !

Système d’équations non-linéaires

Lorsque plusieurs noeuds sont à des pressions différentes $p_i$ et que l’on souhaite connaître la pression $p$ au point milieu ainsi que les débits $Q_{\text{v}i}$ qui en découlent,comme présenté sur la figure qui suit.

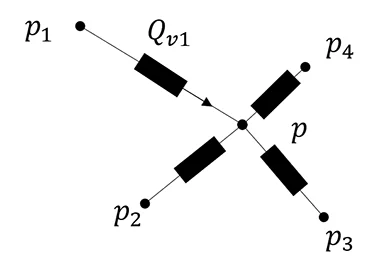
On doit donc résoudre les équilibres des pressions et débits ainsi que la conservation de la masse (somme algébrique des débits nulle). Ceci nous donne le système non-linéaire suivant où \(p\) et les \(Q_{\text{v}i}\) sont les inconnues :

$$ (p_1 - p) = Z_1 Q_{\text{v}1}^2 $$

$$ (p_2 - p) = Z_2 Q_{\text{v}2}^2 $$

$$ (p_n - p) = Z_n Q_{\text{v}n}^2 $$

$$ Q_{\text{v}1} + … +Q_{\text{v}n} = 0 $$

Cette résolution brute ne converge pas toujours car dans certains cas il n’y a pas de solution telle que la pression centrale soit comprise entre les bornes des pressions extérieures. Ceci est dû au fait que la formulation en débit au carré réduit l’espace des solutions à celles qui sont positives ! On pourrait cependant contourner le problème en gardant le même système, à condition que $Z_i$ prenne le signe de $Q_{\text{v}i}$.

Le système suivant, où les débits $Q_{\text{v}i}$ ne sont pas élevés au carré, est une manière simple de laisser libre le signe des solutions (on notera l’astuce de la valeur absolue de la racine) :

$$ \frac{p_1-p}{\sqrt{|p_1 - p|}} = \sqrt{Z_1} Q_{\text{v}1} $$

$$ \frac{p_2-p}{ \sqrt{|p_2 - p|}} = \sqrt{Z_2} Q_{\text{v}2} $$

$$ \frac{p_n-p}{ \sqrt{|p_n - p|}} = \sqrt{Z_n} Q_{\text{v}n} $$

$$ Q_{\text{v}1} + … +Q_{\text{v}n} = 0 $$

La fonction fsolve de Scilab résout avantageusement ce genre de systèmes non-linéaires.

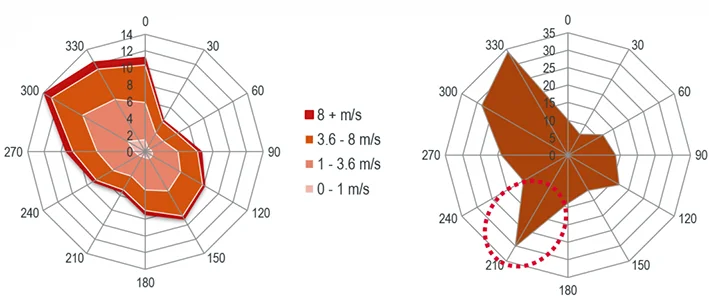
Un exemple d’application est donné sur la figure ci-dessous : à partie de la rose des vents (à gauche), on aura calculé les pressions en façade d’un bâtiment puis la rose des débits (à droite) qui en découle, à l’aide de la méthode décrite dans cet article.