Pluie entraînée par le vent
Introduction
Le phénomène de pluie battante correspond à la combinaison des effets de la pluie avec ceux du vent. Ce phénomène peut être à l’origine de nombreux désordres tels que
- la pénétration de la pluie [Peerez-Bella et al. 2013]1,
- les dommages causés par le gel [Frank et al. 1995]2[Zhou et al. 2020]3,
- la décoloration par efflorescence du sel [Granneman et al. 2019]4,
- la fissuration structurelle due à des gradients thermiques et d’humidité [Annila et al, 2017]5[Slusarek, 2020]6,
- ou encore la saleté des façades par lessivage des matériaux [Blocken et al., 2013]7.

Figure d’après [White, 1967]8
Nous présentons dans cet article une méthode pour évaluer l’exposition à la pluie d’un bâtiment dans son environnement urbain en s’appuyant sur la CFD. Il sera ainsi possible de déterminer les risques auxquelles sont exposées les façades et de mettre en place des solutions préventives ou d’en vérifier leur efficacité.
Nous n’aborderons pas la physique des nuages et des gouttes de pluie, les phénomènes de surface tels que les éclaboussures, le ruissellement, l’évaporation et l’absorption, les mécanismes de la pénétration de la pluie dans les bâtiments ou l’élaboration et l’exécution de tests d’étanchéité.
Dans un premier temps, nous reviendrons sur le phénomène météorologique de la pluie. Nous verrons ensuite comment la combinaison “pluie + vent” est modélisée. Nous proposerons alors un cas d’étude sur lequel nous conduirons une analyse de sensibilité.
Phénomène météorologique de pluie
Définitions
La pluie est le phénomène par lequel les gouttes d’eau liquide tombent des nuages vers le sol. Il s’agit de la forme la plus commune de précipitations sur Terre. Lorsque le diamètre des gouttes est inférieure à \(\phi\) = 0,5 mm, la précipitation est appelée bruine.
On caractérise le volume de précipitation qui atteint une certaine zone au cours d’un certain laps de temps par son intensité. Ainsi, l’intensité de la pluie s’exprime en millimètre par heure [mm/h] ou en litre par mètre carré par heure [l/m²/h].
Distribution des gouttes d’eau
Les gouttes d’eau qui constituent la pluie peuvent être de forme et de taille variable au cours d’un épisode pluvieux.
Forme
Les gouttes ont tendance a être plutôt sphérique pour de petits diamètres. Au contraire, les plus grosses gouttelettes se présentent plutôt comme des sphéroïdes oblats.

Figure d’après [Beard et al., 2010]9
Cette variation de forme a des conséquences importantes sur la vitesse de chute limite des gouttes d’eau.
Aini, en l’absence de vent, une goutte d’eau sera seulement soumise à la force de traînée \(\bar{f}_{\text{D}}\) et la force de gravité \(\bar{f}_{\text{G}}\) données par :
$$ \left|\left|\bar{f}_{\text{G}}\right|\right| = \rho g \pi \frac{\phi^3}{6} \text{ (1)} $$
$$ \left|\left|\bar{f}_{\text{D}}\right|\right| = \frac{1}{2} \rho A C_{\text{d}} V^2 $$
Où $\rho$ est la masse volumique de l’eau, $g$ est l’accélération due à la pesanteur, $\phi$ est le diamètre de la goutte, $A$ est la géométrique qu’offre la goutte à l’écoulement, $C_{\text{d}}$ le coefficient de trainée et $V$ la vitesse de chute.
Lorsque $\left|\left|\bar{f}_{\text{G}}\right|\right| \ll \left|\left|\bar{f}_{\text{D}}\right|\right|$ la goutte accélère et la vitesse de chute augmente jusqu’à atteindre une vitesse de chute limite, dite “vitesse terminale”, $V_{\text{t}}=\sqrt{\frac{2 \ \left|\left|\bar{f}_{\text{G}}\right|\right|}{\rho \ A \ C_{\text{d}}}}$ lorsque $\left|\left|\bar{f}_{\text{G}}\right|\right| = \left|\left|\bar{f}_{\text{D}}\right|\right|$.
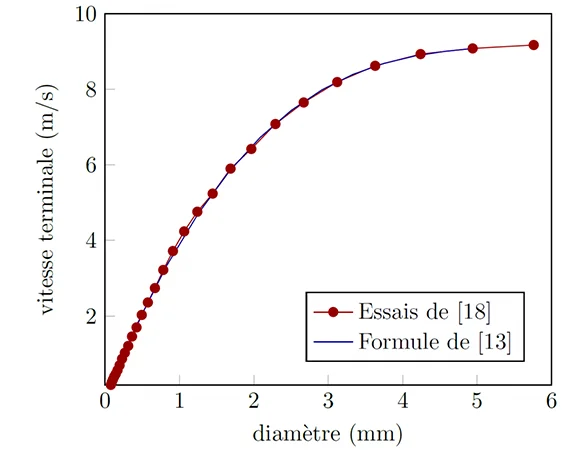
Les auteurs de [Gunn et al. 1949]10 ont réalisé des essais qui ont permis de tracer la courbe rouge dans la figure précédente. On remarque que pour des gouttes dont le diamètre excède 4mm, la vitesse terminale n’augmente pas considérablement en augmentant le volume. Cette tendance s’explique par le changement de forme de la goutte. En effet, pour un sphéroïde oblate accroit la force de traînée qui augmente alors plus vite que les effets de la pesanteur lorsque le diamètre augmente. Ainsi, les gouttes de quatre millimètres et six millimètres présentent des vitesse terminales similaires.
Les auteurs de [Dingle et al., 1972]11 proposent une expression analytique permettant de calculer simplement la vitesse terminale des gouttes d’eau en fonction de leur diamètre $\phi$ :
$$ V_{\text{t}}(\phi) = -0,166033+4,91844 \phi -0,888016 \phi^2 +0,054888 \phi^3 \text{ (2)} $$
Cette équation, précise à \(\pm\) 2 % est valable pour des diamètres \(\phi \le\) 5,8 mm (courbe bleue, figure 3).
Taille
Les gouttes de pluie possèdent non seulement une très large variété de formes, mais également une large gamme de tailles.
Il est communément admis dans la communauté scientifique que la distribution des taille de gouttes peut être approximée par une fonction de l’intensité de la pluie.
De nombreux chercheurs [Laws et al., 1943]12 [Marshall et al. 1948]13 [Best, 1950]14 [Fujiwara, 1961]15 ont réalisé des mesures et développé leur propre modèle. Ils ont montré que la distribution cherchée variait également en fonction du type de tempête, de la hauteur des nuages… On pourra cependant s’appuyer sur les travaux de [Best, 1950]14 qui proposent une expression de la loi de probabilité cumulée de la distribution des tailles de gouttes en fonction de l’intensité de la pluie.
$$ \left(\theta\right) = 1-\exp\left[-\left(\frac{\phi}{A r_{\text{h}}^p}\right)^n\right] \text{ (3)} $$
Où $r_{\text{h}}$ est l’intensité de la pluie, $A$ , $p$ et \(n\) sont des constantes pouvant être prises égales aux valeurs moyennes \(A\) = 1,30, \(p\) = 0,232 et \(n\) = 2,25 calculées par [Best, 1950]14.
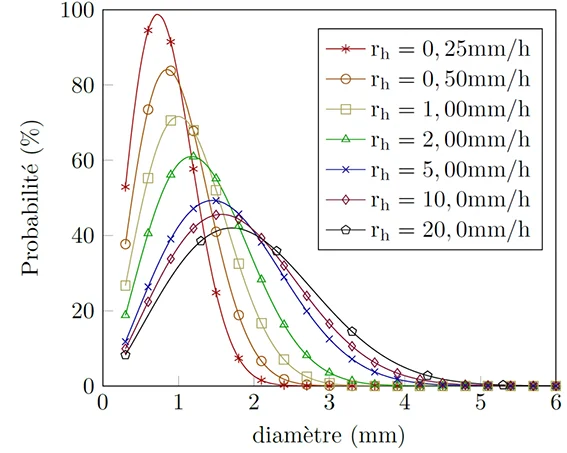
La figure 4 indique que pour une faible intensité de pluie, par exemple \(r_{\text{h}}\) = 0,25 [mm/h], beaucoup de gouttes sont situées entre 0 et 2 [mm] de diamètre. Pour des intensités de pluie plus élevées, par exemple \(r_{\text{h}}\) = 20 [mm/h], la fraction de grosses gouttes est plus élevée.
Couplage pluie et vent
Dans le cas de la pluie entrainée par le vent, la combinaison du vent avec la pluie procure aux gouttelettes une composante de vitesse horizontale non nulle. La pluie dévie alors de sa trajectoire et est projeté sur les façade du bâtiment (figure 5).
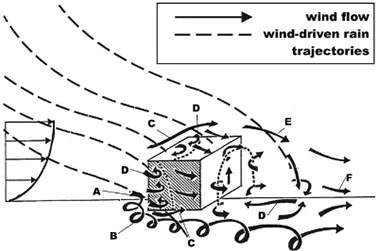
Figure d’après [Blocken et al., 2004]16
En raison des caractéristiques spécifiques de l’écoulement a proximité d’un bâtiment, le cours des gouttelettes de pluie est modifié, ce qui entraîne un mouillage non uniforme de la façade. En effet, lorsque le vent s’approche d’un bâtiment, une perturbation est générée et un schéma d’écoulement spécifique se développe autour de celui-ci , comprenant un vortex frontal (A), des courants d’angle (B), une séparation aux angles des bâtiments (C), des zones de recirculation (D), des couches de cisaillement (E) et un sillage lointain (F).
Vecteurs d’intensité de pluie
L’occurrence conjointe du vent et de la pluie est à l’origine d’un vecteur d’intensité de pluie oblique.
Ce vecteur oblique est parfois appelé pluie battante, ou plus généralement, pluie entrainée par le vent (WDR pour wind driven rain). Ainsi, l’expression intensité de pluie entrainée par le vent se réfère généralement au vecteur pluie oblique ($R$). Ce vecteur est défini pour chaque diamètre de goutte de pluie. Sa taille est égale à la fraction de l’intensité de la pluie pour ce diamètre spécifique et sa direction est donnée par la trajectoire de la pluie entrainée par le vent.
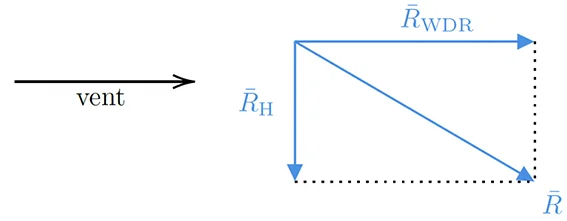
Figure d’après [Blocken et al., 2004]16
Cependant, pour traiter de l’interaction entre la pluie et les façades verticales des bâtiments on se réfère à la décomposition illustrée par la figure 6. Le terme intensité de pluie entrainée par le vent (WD) correspond alors à la composante horizontale du vecteur d’intensité de la pluie oblique ($R_{\text{WDR}}$), qui provoque un flux de pluie à travers un plan vertical7. L’autre composante, verticale, du vecteur d’intensité de la pluie oblique ($R_{\text{H}}$), qui provoque un flux de pluie à travers un plan horizontal, est appelée intensité de la pluie (horizontale). Ce dernier ecteur $R_{\text{H}}$ correspond à l’intensité régulière des précipitations $\left|| R_{\text{H}} \right|| = r_{\text{h}}$, telle que mesurée par les stations météorologiques.
[Hoppestad, 1955]17 proposent la relation suivante pour relier la vitesse du vent $U$ à l’intensité de la pluie $r_{\text{h}}$.
$$ r_{\text{wdr}}= r_{\text{h}} \frac{U}{V_{\text{t}}(\phi)} \text{ (4)} $$
Où $r_{\text{wdr}}= \left|| R_{\text{WDR}} \right||$ peut être compris comme la proportion de pluie passant à travers un plan vertical [l/m²/h].
Charge de pluie entrainée par le vent
Plusieurs quantités existent pour décrire la charge de pluie entrainée par le vent sur les façades. Parmi ces dernières, les plus utilisées sont le taux de capture spécifique $\eta_\phi$, lié au diamètre des gouttes de pluie, et le rapport de taux $\eta$ ; lié à l’ensemble du spectre des diamètres de gouttes de pluie [Blocken et al., 2004]16.
Ces taux de captures sont définis à un instant $t$ comme le rapport entre l’intensité de pluie entraînée par le vent $r_{\text{wdr}}$ et l’intensité de la pluie (horizontale) $r_{\text{h}}$ pour un diamètre $\phi$ de goutte où l’ensemble du spectre.
$$ \eta_\phi\left(\phi,t\right) = \frac{r_{\text{wdr}}\left(\phi,t\right)}{r_{\text{h}}\left(\phi,t\right)} \text{ (5)} $$
$$ \eta\left(t\right) = \frac{r_{\text{wdr}}\left(t\right)}{r_{\text{h}}\left(t\right)} $$
En pratique, ces ratios seront calculés ou mesurés pour des pas de temps discrets. Ils s’écrivent dans ce cas :
$$ \eta_\phi\left(\phi,t_j\right) = \frac{\int_{t_j}^{t_j+\Delta t} r_{\text{wdr}} \left(\phi,t\right) dt}{\int_{t_j}^{t_j+\Delta t} r_{\text{h}} \left(\phi,t\right) dt} \text{ (6)} $$
$$ \eta\left(t_j\right) = \frac{\int_{t_j}^{t_j+\Delta t} r_{\text{wdr}} \left(t\right) dt}{\int_{t_j}^{t_j+\Delta t} r_{\text{h}} \left(t\right) dt \frac{U}{V_{\text{t}}(\phi)}} $$
Les taux de capture sont des fonctions complexes de l’espace et du temps. Six paramètres fondamentaux les influencent dont la géométrie du bâtiment – y compris la topologie de l’environnement – (i), la position sur la façade du bâtiment (ii), la vitesse du vent (iii), la direction du vent (iv), l’intensité (horizontale) des précipitations (v) et la distribution (horizontale) de la taille des gouttes de pluie (vi). Bien que souvent négligée, on pourrait également citer la dispersion turbulente des gouttes de pluie comme paramètre supplémentaire.
Méthodes de calcul semi-empiriques
Les données météorologiques classiques mesurées dans les stations météo sont la direction du vent et sa vitesse ainsi que l’intensité de la pluie ($r_{\text{h}}$).
Les chercheurs ont donc souhaité calculer l’exposition des façades des bâtiments à la pluie entraînée par le vent à partir de ces données météorologiques. Ils ont alors établi des relations semi-empiriques en constant par l’expérience des rapports de proportionnalité entre, d’une part, l’intensité de pluie WD et d’autres parts, la vitesse du vent et l’intensité de pluie mesurée. Les méthodes de calculs existantes dérivent majoritairement de deux approches initiées par [Hoppestad, 1955]17 : l’indice de pluie WD et la formule de pluie WD.
Indice de pluie $WD$
L’indice de pluie entrainée par le vent est calculé comme le produit de la vitesse du vent et de l’intensité de pluie mesurée ($r_{\text{h}}$). Cet indice est approximativement proportionnel à l’intensité de pluie WD ($r_{\text{wdr}}$). Dans sa forme originale, il s’agit d’une mesure qualitative de l’exposition d’un lieu à l’intensité de pluie WD libre, c’est à dire loin de tout obstacle.
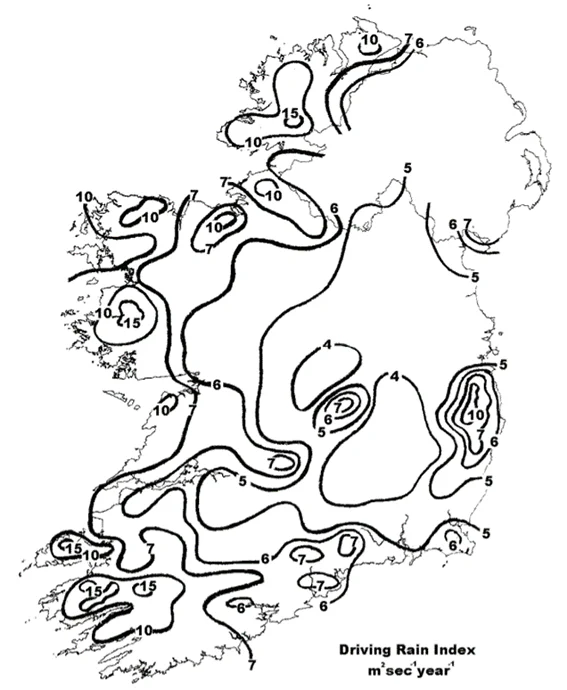
A sa création, l’indice comportait un certain nombre de défauts [Blocken et al., 2004]16 : basé sur des valeurs moyennes annuelles, l’indice de pluie WD est un indice de longue durée (i). Il doit donc être associé à des événements de longue durée tels que l’accumulation d’humidité dans les matériaux poreux, mais pas à des événements de court terme tels que la pénétration à travers les fenêtres (ii). L’indice WDR se rapporte au WDR libre et ne tient donc pas compte des phénomènes locaux induits par la topographie et le bâtiment (iii).
De nouveaux développements et améliorations au cours des dernières décennies ont transformé l’indice en une mesure quantitative de l’exposition d’un mur de bâtiment à la pluie entraînée par le vent. Pour cela des données horaires sur le vent et la pluie furent introduites dans le calcul des indices (i). Un second indice a été juxtaposé à l’indice annuel moyen pour représenter les événements WDR de courte durée (ii). Des facteurs empiriques ont été ajouté pour tenir compte de l’effet de la rugosité du terrain, de la topographie locale, des obstructions et de la géométrie des bâtiments (iii).
Relation de la pluie $WD$
La relation de la pluie WD est une formule reliant l’intensité de la pluie WD aux variables usuelles que sont la vitesse, la direction du vent et l’intensité des précipitations $r_{\text{h}}$ par l’introduction d’un coefficient de pluie WD. Basée sur l’équation (4) qui fournit une estimation de l’intensité de pluie WD libre, [Lacy, 1965]18 propose une valeur au coefficient de pluie WD en retenant la taille médiane des gouttes de pluie. La relation (4) devient alors $r_{\text{wdr}}=0,222 U r_{\text{h}}$. Ce coefficient de pluie WD est par la suite affiné et intègre les effets de l’orientation du vent sur la façade. La relation s’écrit finalement :
$$ r_{\text{wdr}} = \alpha U r_{\text{h}} \cos \left(\theta\right) \text{ (7)} $$
Où $\theta$ est l’angle entre la direction du vent et la normale au mur et $\alpha$ est le coefficient de pluie WD.
La principale difficulté lié à l’utilisation de le relation (7) est l’obtention d’un coefficient de pluie WD fiable. En effet, il dépend d’un grand nombre de paramètres et est différent pour chaque situation et pour chaque scénario de pluie entrainée par le vent considéré. Un coefficient de pluie WD peut être obtenu par des mesures à court terme ou long terme. Dans le premier cas, on obtient un coefficient de pluie WD qui n’est représentatif que de la période mesurée, dans le second cas, on obtient un coefficient qui n’est représentatif que de la moyenne des situations mesurées.
Méthode PrEN 13013-3
Le projet de norme européenne PrEN 13013-3 prévoit une procédure qui repose à la fois sur l’indice de pluie WD et sur la relation de la pluie WD. Elle utilise intrinsèquement un coefficient de pluie WD adapté qui est déterminé comme le produit du coefficient de pluie WD libre (0,222 s/m) par quatre facteurs de correction déterminés empiriquement. Ces quatre facteurs de correction sont $R$ , facteur de rugosité du terrain ; $T$, facteur de topographie ; $O$, facteur d’obstruction et $W$, facteur de mur.
On obtient alors le coefficient ($\alpha$) de (7). Cette correction rend la formule meilleure que la pratique traditionnelle qui consiste à utiliser la relation de la pluie WD avec un seul coefficient de pluie WD. Cette dernière ne tient en effet pas compte des variations du coefficient de pluie WD avec la géométrie du bâtiment et la position sur la façade du bâtiment.
Toutefois, le projet standard présente également un certain nombre d’inconvénients : il ne peut être appliqué que pour les configurations de bâtiments spécifique [Blocken et al., 2004]16 (i). Les facteurs de murs dans les abaques ne fournissent que des informations limitées sur la variation spatiale à travers la façade (ii). Le coefficient de pluie WD ($\alpha$) est supposé être constant pour une position ixe sur le bâtiment, c’est-à-dire constant dans le temps (iii). Il est supposé que le facteur $\cos \left(\theta\right)$ suffit à rendre compte de l’effet de la variation de la direction du vent (iv).
Modélisation numérique
Modèle Lagrangien ou Eulérien
La méthode la plus courante dans la littérature pour modéliser les conséquences de la pluie entrainée par le vent sur les façades des bâtiments est basée sur l’extension de l’approche de Choi en régime permanent [Choi, 1993]19[Choi, 1994]20 dans le domaine temporel par Blocken et Carmeliet [Blocken et al., 2007a]21, [Blocken et al., 2007b]22. Dans cette approche, la phase de pluie est résolue par une modélisation lagrangienne des gouttes est couplée de manière unidirectionnelle avec le vent, l’effet des gouttes de pluie sur l’écoulement d’air étant ignoré. Cette méthode consiste en cinq étapes :
- La configuration du vent en régime permanent autour du bâtiment est calculée avec des modèles de turbulences RANS 3D en régime permanent .
- Les trajectoires des gouttes de pluie sont obtenues par injection de particules de différentes tailles l’écoulement d’air calculé.
- Le taux de capture spécifique pour chaque taille de goutte de pluie est déterminé ur la base des trajectoires calculées.
- Le taux de capture global est calculé à partir du taux de capture spécifique et de la distribution horizontale de la taille des gouttes de pluie.
- Les données expérimentales de vitesse de vent, de direction de vent et d’intensité de pluie sont combinés aux taux de capture pour obtenir les distributions spatiales et temporelles de pluies entrainées par le vent sur les façades des bâtiments.
Les étapes (2) et (3) impliquent un long processus itératif essai-erreur pour trouver des positions d’injection appropriées pour les gouttes de pluie afin qu’elles couvrent toute la surface de la façade étudiée. Il est important de noter que cette procédure doit être répétée pour chaque combinaison de : taille des gouttes de pluie (i), vent de référence vitesse (ii), et direction du vent de référence afin d’établir un tableau complet des taux de capture pour chaque position de la façade (iii).
L’utilisation d’un modèle eulérien multiphasique les calculs de pluie entrainée par le vent offre une procédure plus rapide, même pour un domaine composé d’un seul bâtiment [Kubilay et al., 2013]23.
Dans les modèles eulériens multiphasiques, la phase de pluie et celle de vent sont considérées comme des milieux continus. Chaque classe de taille de goutte de pluie est traitée comme une phase différente, car chaque groupe de gouttes de pluie de taille similaire interagira avec le champ de vent de façon similaire. Il est alors nécessaire d’imposer une condition limite pour chaque classe de gouttes sans avoir à définir un plan d’injection à positionner correctement. Enfin, à l’image de ce qui est fait dans l’approche lagrangienne, le taux de capture global est calculé en sommant les taux de capture spécifiques à chaque phase.
Equations du Modèle Eulérien Multiphasique
Le Modèle Eulérien Multiphasique décrit dans la suite est celui de développé par [Kubilay et al., 2013]23 [Kubilay et al., 2015]24, et proposé en OpenSource sur le site de [Carmeliet]25.
Modélisation du vent
Les auteurs de [Kubilay et al., 2013]23 proposent de modéliser les écoulements de vent à l’aide d’un modèle 3D RANS en régime avec un modèle de turbulence $k-\varepsilon$ [Markatos, 1986]26 en régime permanent. Les équations du modèle utilisé par [Kubilay et al., 2013]23 sont rappelées ici :
$$ \frac{\partial u_j}{\partial x_j} =0 $$
$$ \frac{\partial \rho_{\text{a}} u_i}{\partial t} + \frac{\partial\left(\rho_{\text{a}} u_i u_j\right)}{\delta x_j} = - \frac{\partial p}{\partial x_i} + \frac{\partial \tau_{ij}}{\delta x_j} $$
$$ \frac{\partial \rho_{\text{a}} k}{\partial t} + \frac{\partial\left(\rho_{\text{a}} k, u_j\right)}{\partial x_j} = \frac{\partial }{\partial x_j} \left[\left(\mu+\frac{\mu_t}{\sigma_k}\right)\frac{\partial k}{\partial x_j}\right] + G_k - \rho_{\text{a}} , \varepsilon $$
$$ \frac{\partial \rho_{\text{a}} \varepsilon}{\partial t} + \frac{\partial\left(\rho_{\text{a}} \varepsilon, u_j\right)}{\partial x_j} = \frac{\partial }{\partial x_j} \left[\left(\mu+\frac{\mu_t}{\sigma_\varepsilon}\right)\frac{\partial \varepsilon}{\partial x_j}\right]+ C_{1_\varepsilon}\frac{\varepsilon}{k}G_k-C_{2_\varepsilon}\rho_{\text{a}}\frac{\varepsilon^2}{k} $$
$$ \mu_t=C_\mu \rho_{\text{a}} \frac{k^2}{\varepsilon} $$
où $\rho_{\text{a}}$ désigne la densité de l’air, $p$ la pression, $\tau_{ij}$ le tenseur des contraintes de Reynolds, $k$ l’énergie cinétique turbulente, $\varepsilon$ la dissipation des turbulences, $\mu$ la viscosité dynamique de l’air, $\mu_t$ la viscosité dynamique turbulente de l’air, $\sigma_k$ le nombre de Prandtl turbulent pour $k$ , $\sigma_\varepsilon$ le nombre de Prandtl turbulent pour $\varepsilon$, $G_k$ la génération d’énergie cinétique turbulente due aux gradients de vitesses moyennes.
Les valeurs suivantes des constantes du modèles sont retenues par [Kubilay et al., 2013]23 : $C_{1_\varepsilon}=1,44$, $C_{2_\varepsilon}=1,92$, $C_{\mu}=0,09$, $\sigma_k=1,0$, $\sigma_\varepsilon=1,3$.
Dans le modèle $k-\varepsilon$, le tenseur des contraintes de Reynolds est modélisé en utilisant la viscosité turbulente, $\mu_t$, supposée être une quantité isotrope. Par conséquent, l’erreur augmente dans les régions où les effets de turbulences anisotropes deviennent relativement importants.
Le rapport volumétrique de la pluie dans l’air est inférieur à $1 \times 10^{-4}$. Par conséquent il est raisonnable de considérer un couplage unidirectionnel entre le vent et les gouttes de pluie [Elghobashi, 1994]27.
Transport des gouttes de pluie
Les équations de conservation de la masse et du moment pour la pluie sont résolues en considérant chaque classe de taille de goutte de pluie comme une phase différente.
Les équations qui régissent chaque phase de la pluie $k$ selon [Kubilay et al., 2015]24 sont les suivantes :
$$ \frac{\delta \rho_{\text{w}}\alpha_k}{\delta t}+\frac{\delta\left(\rho_{\text{w}}\alpha_k u_{kj}\right)}{\delta x_j}=0 $$
$$ \frac{\delta \rho_{\text{w}}\alpha_k u_{ki}}{\delta t}+\frac{\delta\left(\rho_{\text{w}}\alpha_k u_{ki} u_{kj}\right)}{\delta x_j} = \rho_{\text{w}} \alpha_k g + \rho_{\text{w}} \alpha_k \frac{3 \mu}{\rho_{\text{w}} \phi^2} \frac{C_{\text{d}} \mathrm{Re}_{\text{p}_\text{r}}}{4} \left(u_i-u_{ki}\right) $$
Où $\phi$ est le diamètre des gouttes de pluie, \(\alpha_k\) est la fraction volumique de la $k$-ième phase de la pluie, $u_{ki}$ la $i$-ième composante du vecteur vitesse de la $k$-ième phase de la pluie, $u_{i}$ composante du vecteur vitesse du vent, $\rho_{\text{w}}$ la densité des gouttes de pluie, $g$ l’accélération gravitationnelle, $C_{\text{d}}$ le coefficient de traînée. \(\mathrm{Re}_{\text{p}_\text{r}}\) désigne le nombre de Reynolds relatif calculé comme suit :
$$ \mathrm{Re}_{\text{p}_\text{r}}=\frac{\rho_{\text{a}} \phi}{\mu} \left||\bar{u}-\bar{u}_k\right|| $$
Avec $\bar{u}$ le vecteur vitesse du vent et $\bar{u}_k$ le vecteur vitesse de la $k$-ième phase de la pluie.
Les effets de la dispersion turbulente des gouttes de pluie peuvent être introduit dans l’équation de transport en rajouttant un terme dépendant des fluctuation de la vitesse $u^\prime_{ki}$. On obtient alors :
$$ \frac{\delta \rho_{\text{w}}\alpha_k u_{ki}}{\delta t}+\frac{\delta\left(\rho_{\text{w}}\alpha_k u_{ki} u_{kj}\right)}{\delta x_j} +\frac{\delta\left(\rho_{\text{w}}\alpha_k u^\prime_{ki} u^\prime_{kj}\right)}{\delta x_j}= \rho_{\text{w}} \alpha_k g + \rho_{\text{w}} \alpha_k \frac{3 \mu}{\rho_{\text{w}} \phi^2} \frac{C_{\text{d}} \mathrm{Re}_{\text{p}_\text{r}}}{4} \left(u_i-u_{ki}\right) $$
Les auteurs de [Kubilay et al., 2015]24 proposent d’introduire un nouveau coefficient $C_{\text{t}}$ tel que :
$$ C_{\text{t}}^2 = \frac{u^\prime_{ji} u^\prime_{kj}}{u^\prime_i u^\prime_j} = \frac{1}{1+\frac{\tau_{\text{p}}}{\tau_{\text{fl}}}} $$
Où $\tau_{\text{p}}$ désigne le temps de relaxation des particules : vitesse de réponse de l’accélération des particules à la vitesse relative entre la particule et le fluide porteur. $\tau_{\text{fl}}$ désigne l’échelle de temps du fluide : durée de vie caractéristique des grands tourbillons. Pour les plus petites gouttes de pluie, $C_{\text{t}}$ tends vers 1,0 . Dans ce cas, les gouttes de pluie sont davantage influencées par les fluctuations de la vitesse du vent.
Taux de capture
Les taux de capture spécifiques et global représentant la charge de pluie entraînée par le vent sur les façades sont évalués numériquement à partir des expressions suivantes :
$$ \eta_k\left(\phi_k\right) = \frac{\alpha_k \left|| \bar{V}_k(\phi_k) \right|| }{r_{\text{h}} f_{\text{h}}\left(r_{\text{h}}, \phi_k\right)} $$
$$ \eta=\int_k f_{\text{h}}(\phi_k) \eta_k (\phi_k)d \phi_k $$
Où $r_{\text{h}}$ est l’intensité de pluie, $f_{\text{h}}\left(r_{\text{h}}, \phi\right)$ la fonction de distribution en taille des gouttes dont la loi de probabilité cumulée est donnée par l’équation (3) et $\left||\bar{V}_k(\phi)\right||$ la norme du vecteur vitesse de la $k$-ième phase projeté sur la normale à la façade étudiée.
Conditions limites
Vent
En entrée du domaine, la vitesse moyenne des vents est calculée à partir de la formule classique pour la couche limite atmosphérique:
$$ u(z) = \frac{u^*}{\kappa}\ln\left(\frac{z+z_0}{z_0}\right) $$
Avec $u(z)$ la vitesse du vent à la hauteur $z$, $u^*$ la vitesse de frottement de la couche limite atmosphérique, $\kappa$ la constante de von Karman ($0,42$ ici) et $z_0$ la hauteur de rugosité aérodynamique.
Les grandeur de la turbulence $k$ et $\varepsilon$ peuvent être obtenues par les équations.
$$ k = \left(I u\right) ^2 $$
$$ \varepsilon = \frac{u^{*3}}{k \left(z+z_0\right)} $$
Dans lesquelles $I$ correspond à l’intensité turbulente.
Pour finir, des fonctions de parois doivent être correctement définies pour les murs. Pour cela, on pourra se référer aux fonctions de parois classiques telles que celles de [Launder et al., 1983]28. Ces fonctions de paroi pourront être enrichies d’un modèle de rugosité en fonction de la nature des surfaces considérées ans l’étude.
Pluie
Le rapport volumétrique de la phase $\phi$ de la pluie, $\alpha_\phi$, peut être obtenu via l’équation :
$$ \alpha_\phi=\frac{r_{\text{h}} , f(r_{\text{h}}, \phi)}{V_{\text{t}}(\phi)} $$
où $V_{\text{t}}(\phi)$ représente la vitesse terminale d’une goutte de pluie de diamètre $\phi$ approchée avec l’équation (2) et $f(r_{\text{h}}, \phi)$ peut être calculée en dérivant l’équation (3) :
$$ f(r_{\text{h}}, \phi)=\frac{n}{A r_{\text{h}}^p} \exp\left[-\left(\frac{\phi}{A r_{\text{h}}^p}\right)^n\right] \left(\frac{\phi}{A r_{\text{h}}^p}\right)^{\left(n-1\right)} $$
Où $A$, $p$ et $n$ sont des constantes du modèle de [Best, 1950]14 définies plus haut.
La valeur du rapport volumétrique de chaque phase de pluie, $\alpha_\phi$, est imposée à l’entrée du domaine et aux limites supérieures. Pour la vitesse de la phase de pluie on suppose que les frontières du domaine sont suffisamment loin des bâtiments pour que l’écoulement ne soit pas perturbé.
En entrée du domaine, la composante verticale de la vitesse de la phase de pluie correspond à la vitesse terminale $V_{\text{t}}(\phi)$ pour cette phase. Les composantes horizontales de la vitesse de la phase de la pluie en entrée du domaine sont, elles, prises égale aux composantes de la vitesse de vent.
Les conditions limites pour les phases de pluie au niveau du bâtiment, murs et sols sont telles que le gradient normal $\partial\alpha_\phi/\partial \bar{n}$ vaut zéro lorsque le vecteur de vitesse normale du vent est orienté vers l’extérieur du domaine. Au contraire lorsque le vecteur de vitesse normale du vent est orienté vers l’intérieur du domaine, [Kubilay et al., 2013]23 posent $\alpha_\phi=0$.
De telles conditions limites, ne permettent pas de rendre compte de l’interaction entre les gouttes de pluie et les murs. Les gouttes de pluie quittent donc le domaine dès qu’elles touchent un mur, si bien que même en présence de zone de recirculation, aucun flux de pluie entrant dans le domaine n’est modélisé.
J. M. Péerez-Bella, J. Dominguez-Hernandez, B. Rodriguez-Soria, J. J. del Coz-Diaz, and E. Cano-Suñen. Combined use of wind-driven rain and wind pressure to define water penetration risk into building facades: the spanish case. Building and Environment, 64:46-56, 2013. DOI ↩︎
L. Franke, I. Schumann, R. Van Hees, L. Van der Klugt, S. Naldini, K. Van Balen, and J. Mateus. Damage atlas, classification and analysis of damage patterns found in brick masonry. 1995. ↩︎
X. Zhou, J. Carmeliet, and D. Derome. Assessment of risk of freeze-thaw damage in internally insulated masonry in a changing climate. Building and Environment,page 106773, 2020. Lien PDF ↩︎
S. J. Granneman, B. Lubelli, and R. P. van Hees. Mitigating salt damage in building materials by the use of crystallization modifers-a review and outlook. Journal of Cultural Heritage, 40:183-194, 2019. DOI ↩︎
P. J. Annila, M. Hellemaa, T. A. Pakkala, J. Lahdensivu, J. Suonketo, and M. Pentti. Extent of moisture and mould damage in structures of public buildings. Case studies in construction materials, 6:103-108, 2017. Lien PDF ↩︎
J. Slusarek and M. Lupie-zowiec. Analysis of the in uence of soil moisture on the stability of a building based on a slope. Engineering Failure Analysis, page 104534, 2020. DOI ↩︎
B. Blocken, D. Derome, and J. Carmeliet. Rainwater runooff from building facades: A review. Building and Environment, 60:339-361, 2013. Lien PDF ↩︎ ↩︎
R. B. White. The changing appearance of buildings. 1967. ↩︎
K. V. Beard, V. Bringi, and M. Thurai. A new understanding of raindrop shape. Atmospheric research, 97(4):396-415, 2010. DOI ↩︎
R. Gunn and G. D. Kinzer. The terminal velocity of fall for water droplets in stagnant air. Journal of Me- teorology, 6(4):243-248, 1949. Lien PDF ↩︎
N. Dingle and Y. Lee. Terminal fallspeeds of raindrops. Journal of applied meteorology, 11(5):877-879, 1972. DOI ↩︎
J. O. Laws and D. A. Parsons. The relation of raindropsize to intensity. Eos, Transactions American Geophys- ical Union, 24(2):452-460, 1943. DOI ↩︎
J. S. Marshall and W. M. K. Palmer. The distribution of raindrops with size. Journal of meteorology, 5(4):165- 166, 1948. DOI ↩︎
A. Best. The size distribution of raindrops. Quarterly Journal of the Royal Meteorological Society, 76(327):16-36, 1950. DOI ↩︎ ↩︎ ↩︎ ↩︎
M. Fujiwara. Raindrop size distributions with rainfall types and weather conditions. Technical report, Illinois State Water Survey, 1961. Lien PDF ↩︎
B. Blocken and J. Carmeliet. A review of wind-driven rain research in building science. Journal of wind en- gineering and industrial aerodynamics, 92(13):1079-1130, 2004. Lien PDF ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
S. Hoppestad. Driving rain in norway. Norwegian Build- ing Research, 1955. DOI ↩︎ ↩︎
R. E. Lacy. Driving rain maps and the onslaught of rain on buildings. In Proc. of CIB/RILEM Symposium on Moisture Problems in Buildings, Helsinki, 1965, 1965. ↩︎
E. Choi. Simulation of wind-driven-rain around a building. In Computational Wind Engineering 1, pages 721- 729. Elsevier, 1993. Lien PDF ↩︎
E. Choi. Determination of wind-driven-rain intensity on building faces. Journal of Wind Engineering and Industrial Aerodynamics, 51(1):55-69, 1994. DOI ↩︎
B. Blocken and J. Carmeliet. On the errors associated with the use of hourly data in wind-driven rain calculations on building facades. Atmospheric Environment, 41(11):2335-2343, 2007. Lien PDF ↩︎
B. Blocken and J. Carmeliet. Validation of cfd simulations of wind-driven rain on a low-rise building facade. Building and Environment, 42(7):2530-2548, 2007. Lien PDF ↩︎
A. Kubilay, D. Derome, B. Blocken, and J. Carmeliet. Cfd simulation and validation of wind-driven rain on a building facade with an eulerian multiphase model. Building and environment, 61:69-81, 2013. Lien PDF ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
A. Kubilay, D. Derome, B. Blocken, and J. Carmeliet. Wind-driven rain on two parallel wide buildings: feld measurements and cfd simulations. Journal of Wind Engineering and Industrial Aerodynamics, 146:11-28, 2015. Lien article ↩︎ ↩︎ ↩︎
J. Carmeliet. Wind-driven rain solver for openfoam. https://carmeliet.ethz.ch/research/downloads/ winddrivenrainfoam.html. Lien PDF ↩︎
N. Markatos. The mathematical modelling of turbulent flows. Applied Mathematical Modelling, 10(3):190-220, 1986. DOI ↩︎
S. Elghobashi. On predicting particle-laden turbulent flows. Applied scientifc research, 52(4):309-329, 1994. Lien PDF ↩︎
B. E. Launder and D. B. Spalding. The numerical computation of turbulent flows. In Numerical prediction of flow, heat transfer, turbulence and combustion, pages 96-116. Elsevier, 1983. Lien PDF ↩︎