Modélisation du confort
La modélisation du confort dans les espaces semi-ouverts, aux conditions ambiantes variables et dont l’occupation peut être transitoire requiert un niveau de détail supérieur à celui généralement utilisé dans le bâtiment. Les approches classiques en régime permanent de type PMV s’avèrent inadaptées à de tels environnements et l’on recourt alors à un modèle transitoire du métabolisme humain. Dans cet article, on présente un indicateur de confort basé sur un tel modèle, ainsi que l’influence de la variabilité physiologique sur celui-ci.
Introduction
De nombreuses approches ont été développées afin de quantifier le niveau de confort des individus dans les espaces intérieurs, souvent à des fins de productivité : les premières études du domaine ont consisté à mettre en regard les températures intérieures d’usines et la qualité de la production ou l’absentéisme1.
Dans certains cas particuliers, la température intérieure de confort peut être déterminée par une méthode empirique. Ainsi l’approche adaptative de [R. De Dear, 2001] utilisée pour les bâtiments en ventilation naturelle donne une relation linéaire entre température de confort et la moyenne glissante sur un mois de la température extérieure, calibrée à partir de milliers de mesures.
En ambiance intérieure, le plus utilisé des indicateurs est le Predicted Mean Vote de [Fanger, 1970]2 qui relie le flux (négatif ou positif) auquel est soumis l’individu à la sensation de confort ou d’inconfort. Le lien a été rendu possible par la combinaison d’une approche équationnelle, permettant d’établir le bilan thermique, avec une régression statistique sur le niveau de confort d’un échantillon de quelques milliers de personnes. Cependant des travaux récents ont montré les limites de l’approche PMV [van Hoof, 2008]3 qui est calée sur une morphologie masculine et occasionne des décalages importants de la plage de confort selon le genre [Kingma, 2015] .
L’approche équationnelle traitée ici est le two-node model développé à la fondation J.-B. Pierce (aussi appelé modèle de Pierce) au courant du XXe siècle [Gagge, 1936]4. Il s’agissait alors de répondre à des besoin militaires, et notamment de déterminer la résistance au stress thermique des soldats ou des pilotes de chasse soumis à des pressions atmosphériques très variables [Nishi, 1977]5. La formulation du modèle est relativement simple et consiste à représenter le corps humain sous la forme de deux cylindres concentriques représentant le centre du corps ou “noyau” et la couche de peau, entourés de la vêture (voir Fig. 1). Dans ce modèle, le métabolisme est un système régulé en température par des actions de correction (vasomotricité, sudation, perspiration) qui évoluent au cours du temps et en fonction des conditions environnantes.

En effet, dans les milieux extérieurs ou semi-extérieurs, les variations rapides des conditions ambiantes rendent les approches en régime permanent inaptes à la prédiction du confort. Ceci est d’autant plus vrai lorsque ces espaces sont occupés de manière transitoire (e.g. les lieux extérieurs de passage, les bâtiments très ouverts, les gares) : le temps de montée en température du métabolisme est de l’ordre d’une heure en été et de plusieurs heures en hiver [Hoeppe, 2002]6.
À titre d’illustration, la Fig. 2 montre la simulation des températures corporelles et de la mouillure cutanée d’un individu avec le modèle à deux noeuds de Pierce. À partir de l’état d’équilibre thermique, l’individu est mis dans un environnement chaud avec un fort rayonnement solaire pour trente minutes. L’évolution des températures corporelles en régime transitoire (lignes continues) montre une évolution asymptotique vers le régime permanent qui serait obtenu dans ces conditions (lignes pointillées). La mouillure cutanée suit quant à elle une dynamique légèrement plus lente et le régime permanent n’est pas atteint en une demi-heure d’exposition.
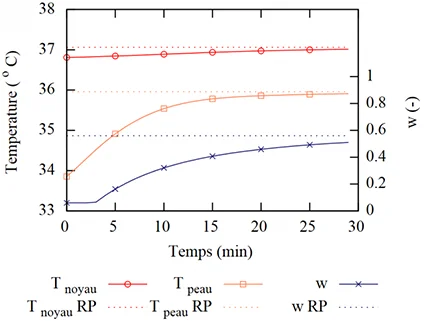
Les réactions physiologiques engendrées par l’environnement sur le métabolisme via convection, rayonnement et échanges hydriques permettent de calculer l’indicateur de confort SET (Standard Effective Temperature). Il s’agit de la température opérative d’un environnement de référence qui produirait la même température de peau et la même mouillure cutanée que l’environnement réel étudié. Cet environnement de référence a une vitesse d’air faible, une humidité relative à 50% et la vêture est standardisée par rapport à l’activité de l’individu.
Les sections qui suivent donnent la description mathématique du corps humain et des transferts associés dans le but de déterminer la SET à partir de ses réactions physiologiques. On abordera ensuite l’effet de l’environnement sur le confort, puis l’influence de la variabilité physiologique sur la dispersion des résultats sera explorée.
Caractéristiques d’activité et de vêture
Dans cette section, les caractéristiques morphologiques de l’humain et de sa vêture sont décrites.
Terme d’activité métabolique
Le métabolisme se décompose entre métabolisme dit “basal”, de maintien en température, et métabolisme d’activité, lié à la tâche effectuée. Le terme d’activité métabolique basale, $M$ [W], est exprimé en fonction de la taille \(H\) [m], de la masse \(m\) [kg] et de l’âge et est calculé avec l’équation ci-dessous issue de [VDI, 2008]7.
$$ M = a \times m^{0,75} \left( 1 + b \times (30,0 - \text{age} ) + c \times \left( \frac{100H}{m^{1/3}} - d \right) \right) $$ Pour les individus masculins et féminins, les constantes $a$, $b$, $c$ et $d$ prennent respectivement les valeurs $a$ = 3,45, $b$ = 0,004, $c$ = 0,01, $d$ = 43 et $a$ = 3,19, $b$ = 0,004, $c$ = 0,018 et $d$ = 42,1.
La surface du corps humain (en m²) est déterminée à partir de l’équation empirique de Dubois qui donne une relation entre taille \(H\) et masse \(m\) :
$$ A = 0,203 \times m^{0,425} \times H^{0,725} $$
La valeur typique pour un individu moyen est $ A \approx$ 1,8 [m²].
Le terme source métabolique peut être donné de deux façons :
- soit directement en [met] avec 1 [met] = 58,2 [W/m²] de surface corporelle. Une activité légère de bureau correspond en général à 1 [met],
- soit en tant que combinaison du métabolisme basal et du métabolisme d’activité lié à l’exécution de la tâche, généralement en [W] que l’on convertit en [W/m²] à l’aide des deux précédentes relations.
Le tableau 1, ci-après, donne quelques ordres de grandeur de la puissance dégagée en fonction de l’activité.
| Activité | [W/m²] | [met] |
|---|---|---|
| Repos, Couché | 45 | 0,8 |
| Repos, Assis | 58 | 1 |
| Debout, Activité légère (bureau) | 70 | 1,2 |
| Travail léger debout (laboratoire) | 95 | 1,6 |
| Activité moyenne debout (travail sur machine) | 115 | 2 |
| Activité soutenue (travail lourd) | 175 | 3 |
Table 1 : Métabolisme en fonction de l’activité
Propriétés de la vêture
La vêture est prise en compte via une résistance thermique $i_{\text{clo}}$ exprimée en [clo], tel que 1 [clo] = 0,155 [m².K/W] (notée $R_\text{cl}$ dans cette unité).
À titre d’exemple, la valeur de 1 [clo] correspond à un costume chemise/veste/pantalon. La table 2, ci-dessous donne le niveau d’isolation en [clo] pour quelques ensembles de vêtements.
| Vêture | [clo] |
|---|---|
| Tenue d’été légère | 0,3 |
| Tenue de travail de bureau | 0,7 |
| Tenue d’intérieur d’hiver | 1,0 |
| Tenue extérieure typique | 1,5 |
Table 2 : Correspondance entre vêture et niveau d’isolation en clo
Le port de vêtements augmente la résistance thermique entre l’environnement extérieur et la surface de la peau. Cependant il augmente également la surface exposée au transfert de chaleur : on introduit alors le facteur $f_{\text{clo}}$ afin de caractériser l’augmentation de la surface d’échange liée à la vêture :
$$ f_{\text{cl}} = 1 + k \times i_{\text{clo}} $$
Dans l’équation précédente, $k$ = 0,2 si $i_{\text{clo}}$ < 0,5 et $k$ = 0,15 sinon. La surface $A \times f_{\text{cl}}$ se trouve ainsi augmentée de 20% pour le port d’une résistance thermique de 1 [clo].
La quantité de vêtement portée varie en fonction de la saison et de facteurs individuels. Cependant les travaux de [Schiavon, 2013]8 ont montré que le niveau de vêture des individus peut être déterminé à partir de la température extérieure à 6 heures du matin le jour même, selon la loi représentée sur la Fig. 3.
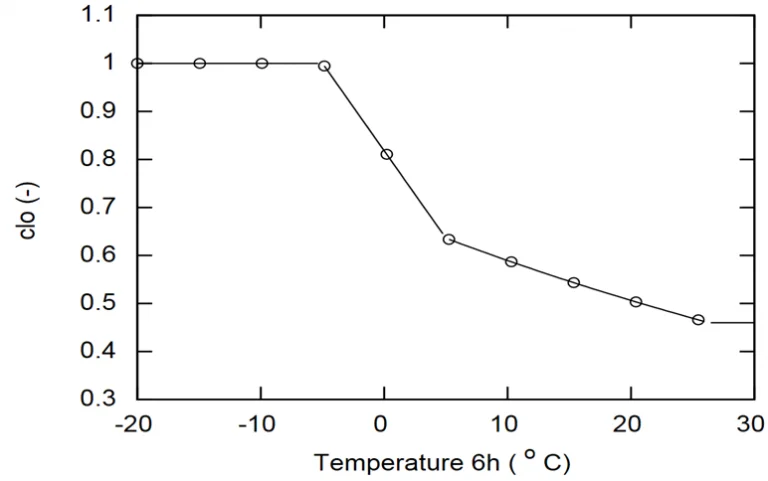
Mise en équation du métabolisme humain
Dans cette section, le bilan des flux sur les deux nœuds du modèle de Pierce est exposé. On détaille ensuite le calcul des transferts de chaleur et de masse sur le corps humain puis la régulation des températures métabolique. Enfin, le calcul de la SET sera explicité.
Équations gouvernantes du modèle de Pierce
Le modèle à deux-nœuds de [Gagge, 1971]9 considère le corps humain comme deux cylindres concentriques (noyau et peau) régulés en température par plusieurs mécanismes : perspiration, sudation, frissonnement, vasomotricité. La chaleur métabolique ainsi que l’énergie dissipée du fait de l’activité sont représentés par un terme source. Deux équations-bilan permettent de calculer l’évolution des température du noyau de la peau en fonction des transferts radiatifs, convectifs et évaporatifs avec le milieu extérieur (la conduction est négligée pour la posture debout, la surface de contact avec le sol étant de l’ordre de 2% de celle du corps). La Fig. 4, ci-dessous, donne un représentation du modèle cylindrique et des flux appliqués :
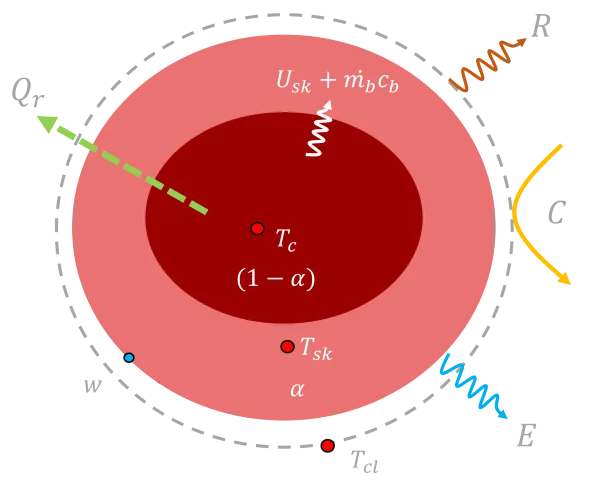
On établit alors un bilan de puissance sur le noyau, tel que la somme algébrique de la puissance métabolique $M$, de la puissance échangée avec la couche de peau (conduction \(U_{\text{sk}}\) et débit sanguin \(\dot{m_{\text{b}}} c_{\text{b}}\)) et des échanges respiratoires \(Q_{\text{r}}\) soit égale à une accumulation de puissance dans le noyau \(S_{\text{c}}\) (indice “c” pour core).
$$ M - \left( U_{\text{sk}} + \dot{m_{\text{b}}} c_{\text{b}} \right) \left( T_{\text{c}} - T_{\text{sk}} \right) - Q_{\text{r}} = S_{\text{c}} $$
Dans l’équation ci-dessus, le terme $M$ correspond à l’activité métabolique en [W/m²], $U_\text{sk}$ est la conductance thermique des tissus entre le noyau et la peau (prise telle que $U_\text{sk}$ = 5,28 [W/(m².K)]). $\dot{m}c_{\text{b}}$ représente le produit du débit massique sanguin $\dot{m}$ et de la capacité thermique massique du sang $c_{\text{b}}$ = 4180 [J/(kg.K)]. $Q_{\text{r}}$ est la puissance totale dissipée par la respiration (sensible et latente).
À la surface de la peau, l’accumulation $S_{\text{sk}}$ (skin) est la somme de la puissance transférée depuis le noyau par conduction et par le débit sanguin, des apports convectifs $C$, radiatifs $R$ et évaporatifs $E$ :
$$ \left( U_{\text{sk}} + \dot{m_{\text{b}}} c_{\text{b}} \right) \left( T_{\text{c}} - T_{\text{sk}} \right) - C - R - E = S_{\text{sk}} $$
Dans l’équation ci-dessus, le terme de droite représente l’accumulation d’énergie dans la couche de peau. À gauche de l’égalité, le terme $E$ représente les échanges évaporatifs à la surface de la peau liés à la perspiration et à la sudation. Les termes $C$ et $R$ représentent respectivement les échanges convectifs et radiatifs. Le schéma électrique équivalent est donné ci-dessous :

La masse de la peau varie en fonction du débit sanguin qui gonfle plus ou moins les tissus externes. On introduit donc la fraction $\alpha$ de la masse corporelle contenue dans le cylindre extérieur du modèle. Les variations des températures de peau \(T_{\text{sk}}\) et du noyau \(T_{\text{c}}\) sont alors décrites par les équations différentielles ci-dessous :
$$ S_{\text{sk}} = \alpha \times \frac{mc_{\text{p}}}{A} \frac{dT_{\text{sk}}}{dt} $$
$$ S_{\text{c}} = (1-\alpha) \times \frac{mc_{\text{p}}}{A} \frac{dT_{\text{c}}}{dt} $$
Dans la seconde équation, la capacité thermique massique du corps vaut $c_{\text{p}}$ = 3492 [J/(kg.K)], le coefficient $\alpha$ représente la fraction de la masse du corps constituée par la peau, celle-ci variant en fonction du débit sanguin. La Fig. 4 montre le modèle dans son ensemble.
Note : Le pourcentage de masse graisseuse $G$ du corps humain peut être pris en compte en pondérant les capacités thermiques des tissus, de sorte que: $$ c_{\text{p}} = G \times c_{\text{g}} + (1-G) \times c_{\text{b}}$$ avec respectivement $c_{\text{g}}$ = 2510 [J/kg/K] la capacité thermique massique de la graisse et $c_{\text{b}}$ = 3650 [J/kg/K] celle des tissus.
En posant pour conditions initiales de $T_\text{sk}$,$T_\text{c}$ les valeurs de consigne $T_\text{sk}^\text{set}$, $T_\text{c}^\text{set}$, il est possible de résoudre les deux équations différentielles temporelles du modèle à deux nœuds. Le modèle régi par ce système donne ainsi l’évolution des températures corporelles en fonction des échanges avec le milieu environnant. Le calcul des différents termes présentés dans les bilans ci-avant sont explicités dans les sections qui suivent.
Échanges respiratoires
Le débit de ventilation pulmonaire est donné en fonction de l’activité métabolique en met tel que :
$$ \dot{m}_{\text{p}} = 0,3 \times \text{met } \text{ [kg/m$^2$/s]} $$
Si on convertit pour un calcul direct avec $M$ en $[\text{W/m}^2]$ et un débit en $[\text{kg/s}]$, il vient avec 1 $[\text{met}]$ = 58,2 $[\text{W/m}^2]$ :
$$ \dot{m}_{\text{p}}= M \times \frac{0,3}{58,2 \times 3600} = M \times 1,432 \times 10^{-6} \text{ [kg/m$^2$/s]} $$
La température de l’air expiré est donnée par la corrélation suivante :
$$ T_\text{exp}= 32,5 + 0,066 \times T_{\text{a}} + 1,99 \times 10 ^{-6} \times p_{\text{a}} $$
où $T_{\text{a}}$ est la température d’air et $p_{\text{a}}$ est la pression de vapeur de l’air ambiant en [Pa].
L’énergie sensible dissipée vaut alors :
$$ C_{\text{resp}} = \dot{m_{\text{p}}} c_{\text{p}} \times ( T_{\text{exp}} - T_{\text{a}} ) $$
Avec $c_{\text{a}}$ = 1006 [J/(kg.K)] pour l’air on retrouve l’équation bien connue [Thellier, 1989] ,[Fanger, 1970]2 :
$$ C_\text{resp} = 1,432 \times 10^{-3} M \times (T_\text{exp}- T_{\text{a}}) \text{ [W/m$^2$]} $$
La formulation ci-dessus, pourtant très usitée, omet de prendre en compte l’énergie sensible soutirée par l’élévation de température de la vapeur d’eau $w_{\text{a}}$ [kg/kg] contenue dans l’air expiré. Une expression rigoureuse des pertes sensibles par respiration, tenant compte de la chaleur spécifique de la vapeur $c_{\text{v}}$ est la suivante :
$$ C_{\text{resp}} = \dot{m}_{\text{p}} \times \left( c_{\text{a}} + w_{\text{a}}c_{\text{v}} \right) \times \left( T_{\text{exp}} - T_{\text{a}}\right) $$
L’énergie latente dissipée se calcule d’après la différence d’humidité absolue des poumons $w_\text{exp}$ et de l’air ambiant \(w_{\text{a}}\) :
$$ E_{\text{resp}} =\dot{m}_{\text{p}} L_{\text{v}} (w_{\text{exp}}- w_{\text{a}}) $$
Il est plus commun de travailler avec des pressions de vapeur qu’avec l’humidité absolue de l’air. Nous convertissons donc l’équation précédente avec les relations psychrométriques. D’après la loi des gaz parfaits on sait que le contenu en humidité de l’air dépend de la pression atmosphérique $p_\text{atm}$ et du rapport des masses molaires de l’air $M_\text{a}$ et de la vapeur d’eau $M_{\text{v}}$ :
$$ w = \frac{M_{\text{v}}}{M_\text{a}}\times \frac{p_{\text{a}}}{p_\text{atm} - p_{\text{a}}} \simeq 0,622 \times \frac{p_{\text{a}}}{p_\text{atm} - p_{\text{a}}} \text{ [kg/kg]} $$
Ainsi l’équation de l’énergie latente dissipée devient :
$$ E_{\text{resp}} = 0,622 \times \dot{m}_p L_{\text{v}} \times \Big (\frac{p_\text{a}}{p_\text{atm} - p_\text{a}} - \frac{p_\text{v exp}}{p_\text{atm} - p_\text{v exp}} \Big ) \text{ [W/m$^2$]} $$
La pression de vapeur de l’air expirée est \(p_\text{v exp}\) et à pression de vapeur saturante $p_\text{v exp} = p_\text{vs}(T_\text{exp})$ avec la corrélation suivante pour la pression de vapeur saturante :
$$ p_\text{vs}(T) = 10^{\frac{2,7877 + 7,625 \times T }{241 + T}} $$
En général la relation précédente est simplifiée en considérant que les pressions de vapeur expirée et ambiante (de l’ordre de $3.10^3$ [Pa]) sont faibles devant la pression atmosphérique qui est de l’ordre de $10^5$ [Pa]. Ainsi on pose :
$$ p_\text{atm} - p_\text{v} \simeq p_\text{atm} - p_\text{v exp} \simeq p_\text{atm} $$
L’énergie latente dissipée devient alors :
$$ E_\text{resp} \simeq 0,622 \times \frac{\dot{m}_{\text{p}} L_{\text{v}} }{p_\text{atm}}(p_\text{v exp}- p_{\text{a}}) $$
$$ E_\text{resp} \simeq 2,14 \times 10^{-5} \times M \times (p_\text{v exp}- p_{\text{a}}) \text{ [W/m$^2$]} $$
L’influence des simplifications réalisées, en négligeant la chaleur sensible de la vapeur d’eau et avec l’hypothèse de faibles pressions expirées devant la pression atmosphérique, sont limitées : selon les conditions de température et d’humidité considérées, le biais introduit est de l’ordre de 2% à 7% entre formulations exactes et approchées des pertes sensibles et latentes (la répartition des pertes est donnée sur la Fig. 6. Cette déviation peut s’avérer non-négligeable dans la mesure où les pertes par respiration atteignent entre $\sim$ 25% et 30% du métabolisme au repos (à ce sujet, voir l’expérimentation de [Cain, 1989]10). On pourra s’aider de la Fig. 6 donnant l’erreur entre formulations pour déterminer s’il est nécessaire d’utiliser les équations exactes.
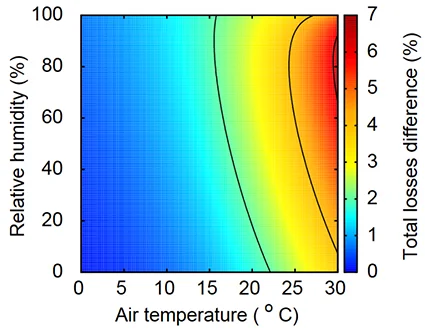
Transfert de chaleur
Cette section présente les échanges convectifs et radiatifs du corps avec l’environnement.
Échanges convectifs
L’échange en convection naturelle est calculé à partir de la corrélation suivante, qui pondère le coefficient de convection en fonction de la pression ambiante :
$$ h_{\text{c}}=3\times p_\text{atm}^{0,53}\text{ [W/(m$^2$.K)]} $$
Lorsque la vitesse d’air $v$ est connue, on utilise la corrélation suivante, fonction de la vitesse et de la pression atmosphérique illustrée sur la Fig. 7 :
$$ h_{\text{c}} = 8,6 \times (v \times p_\text{atm}\times 10^{-5})^{0,53} \text{ [W/(m$^2$.K)]} $$
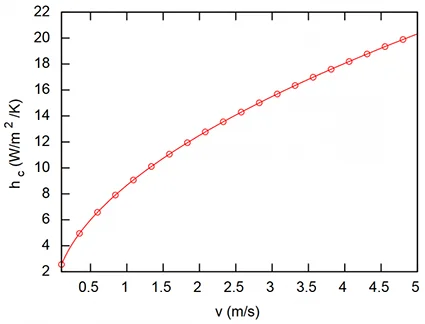
En pratique on prend comme coefficient d’échange la valeur maximum entre les deux équations précédentes. La littérature est prolixe en corrélations pour le calcul du coefficient d’échange onvectif sur l’être humain, à ce sujet on pourra voir aussi la synthèse faite par [Thellier, 1989] .
Échanges radiatifs
Les transferts radiatifs de grande longueur d’onde, ou infra-rouges, entre la surface à température $T$ et les parois environnantes à température $T_{\text{r}}$ sont modélisés via un coefficient d’échange radiatif linéarisé $h_{\text{r}}$ déterminé comme suit :
$$ R = \sigma \varepsilon f (T^4 - T_{\text{r}}^4) $$
$$ R = \sigma \varepsilon f (T^2 - T_{\text{r}}^2) (T^2 + T_{\text{r}}^2) $$
$$ R =\sigma \varepsilon f (T - T_{\text{r}})(T + T_{\text{r}}) (T^2 + T_{\text{r}}^2) $$
Où $\varepsilon$ est l’émissivité de la vêture et $f$ est un facteur d’efficacité du rayonnement prenant en compte le fait que certaines surfaces du corps ne sont pas en regard des parois environnantes (dessous des bras, intérieur des jambes).
On pose alors $T_{\text{m}} = (T+T_{\text{r}})/2$, ce qui donne l’équation :
$$ R \simeq \sigma \varepsilon f (T - T_{\text{r}}) \times 2 T_{\text{m}} \times 2 T_{\text{m}}^2 $$
$$ R\simeq 4 \sigma \varepsilon f T_{\text{m}}^3 \times (T - T_{\text{r}}) = h_{\text{r}} \times (T - T_{\text{r}}) $$
Ainsi on obtient le coefficient d’échange radiatif linéarisé $h_{\text{r}}$ :
$$ h_{\text{r}} = 4 \sigma \varepsilon f T_{\text{m}}^3 \text{ [W/(m$^2$.K)] } $$
À température ambiante, avec $\varepsilon$ = 0,97 et $f$ = 0,72, on obtient $h_{\text{r}} \approx 4,7$ [W/(m².K)].
En espace extérieur, l’individu est régulièrement soumis au rayonnement solaire. Une façon simple d’intégrer les flux solaires dans le bilan thermique est de les convertir en élévation de la température moyenne rayonnante. Le flux total absorbé par le corps humain est donc supposé égal à celui provoqué par une température moyenne radiante $T_{\text{r}}^*$ supérieure à $T_{\text{r}}$.
$$ \alpha f_{p} \varphi_0 = \sigma \varepsilon (T_{\text{r}}^{*4}-T_{\text{r}}^4) $$
$$ T_{\text{r}}^{*} = \sqrt[4]{ T_{\text{r}}^4 + \frac{\alpha f_{p} \varphi_0}{\sigma \varepsilon} } $$
Où $\varphi_0$ est le flux sur une surface orthogonale au rayonnement, $\alpha \approx$ 0,7 est le coefficient d’absorption du rayonnement solaire, $f_{\text{p}}$ est un facteur de projection du rayonnement solaire qui dépend de la hauteur solaire \(h\) (une bonne approximation est donnée par $f_{\text{p}} \simeq 0,233 \times \cos(h)+0,067$ d’après [Helbig, 2013]11).
Échange sensible total
Les transferts convectif et radiatif sont regroupés en un terme d’échange de chaleur global $h_{\text{g}}$ :
$$ h_{\text{g}} = h_{\text{r}} + h_{\text{c}} $$
Ainsi la résistance thermique globale vaut, en tenant compte de l’incrément de surface d’échange lié au port de vêtements :
$$ R_\text{g} = \frac{1}{f_\text{cl} h_{\text{g}}} $$
On calcule alors la température opérative $T_\text{op}$, moyenne pondérée des température d’air et de parois telle que :
$$ T_\text{op} = \frac{h_{\text{c}} T_{\text{c}} + h_{\text{r}} T_{\text{r}}}{h_{\text{c}} + h_{\text{g}}} $$
La température opérative peut être interprétée comme la température d’une enceinte où l’air et les parois sont à température égale ( $T_{\text{a}} = T_{\text{r}}$) et où les échanges convectif et radiatif avec l’individu seraient de égaux à ceux de l’environnement réel (dans lequel $T_{\text{a}} \ne T_{\text{r}}$).
La température de vêture $T_\text{cl}$ peut alors être déterminée par un bilan de flux à la surface de la peau et en surface de vêture :
$$ T_\text{cl} = \frac{R_\text{g} T_\text{sk} + R_\text{cl} T_\text{op}} {R_\text{g}+ R_\text{cl}} $$
On notera que la formulation de l’équation précédente est implicite : le coefficient d’échange $h_{\text{r}}$ dépend de la température de surface $T_\text{cl}$ (voir l’équation du coefficient d’échanges radiatifs). De même, la température opérative est également calculée à partir du coefficient d’échange $h_{\text{r}}$ (voir deux équations plus haut), il convient donc d’itérer pour obtenir $T_\text{cl}$.
Transfert de masse
Le transfert de vapeur entre la peau et l’air ambiant, via la couche de vêtement est régi par l’égalité suivante, avec $p_\text{sk} = p_\text{vs}(T_\text{sk})$ la pression de vapeur à saturation à température de peau :
$$ E_\text{max} = \frac{p_\text{sk} - p_\text{a}}{R_{\text{e}}} $$
où $R_{\text{e}}$ est la résistance totale de perméation à la vapeur d’eau entre surface et ambiance, calculée à partir de la formulation suivante :
$$ R_{\text{e}} = \frac{R_{\text{g}} + R_\text{cl}}{LR \times i_{\text{m}}} $$
où $i_{\text{m}}$ est l’indice de perméabilité à l’humidité qui par définition est le rapport entre résistance thermique et résistance au transfert de vapeur multiplié par la relation de Lewis $LR$. On utilise en général $i_{\text{m}}$ = 0,38, cependant pour des vêtures spécifiques cette valeur peut être plus faible. Par exemple pour des habits en PVC souple ou en néoprène $i_{\text{m}} \sim$ 0,15.
La relation de Lewis caractérise le rapport entre transfert de masse et transfert de chaleur. Elle permet de calculer le coefficient de transfert de vapeur à partir du coefficient convectif. En pratique $LR \sim 17 \times 10^{-3}$ [K/Pa], cependant la valeur peut être affectée par des conditions ambiantes particulières. La relation de Lewis ayant un impact conséquent sur le calcul de la SET*, on en présente le calcul dans la section qui suit.
Calcul de la relation de Lewis : $LR$
L’analogie entre transfert de chaleur et de masse permet d’écrire les corrélations suivantes pour les nombres de Nusselt $Nu$ (rapport du transfert de chaleur convectif et conductif à une interface) et de Sherwood $Sh$ (rapport des échanges de masse convectif et diffusif à une interface) :
$$ Nu = C \times Re^m \times Pr ^n= \frac{h_{\text{c}} L_{\text{c}}}{\lambda } $$
$$ Sh = C \times Re^m \times Sc ^n = \frac{\beta L_{\text{c}}}{D} $$
Où $L_{\text{c}}$ est la longueur caractéristique du phénomène, $\beta$ [m/s] est la vitesse de transfert de masse, $D$ [m²/s] est le coefficient de diffusion massique et $\lambda$ [W/(m.K)] est la conductivité du fluide. Le nombre de Prandtl $Pr$ est le rapport de la diffusion de quantité de mouvement sur la diffusivité thermique et le nombre de Schmidt \(Sc\) est son équivalent pour le transfert de masse. On effectue alors le rapport des deux nombres :
$$ \frac{Sh}{Nu}= \Big( \frac{Sc}{Pr} \Big)^n $$
Ainsi en remplaçant les nombres de Sherwood et Nusselt par leurs expressions on obtient le nombre de Lewis $Le$, rapport de la diffusivité thermique $\alpha =\frac{\lambda }{\rho_{\text{a}} c_{\text{a}}}$ sur la diffusivité massique de vapeur dans l’air $D$ :
$$ \frac{\beta L_{\text{c}}}{D} \frac{\lambda }{h_{\text{c}} L_{\text{c}}}= \Big( \frac{Sc}{Pr} \Big)^n = Le^n $$
En reformulant l’expression précédente on peut isoler la vitesse de transfert $\beta$ en [m/s], avec généralement $n=1/3$ :
$$ \beta = \frac{h_{\text{c}} \times Le^{n-1}}{\rho_{\text{a}} c_{\text{a}}} $$
Le débit de vapeur $\dot{m}_v$ est proportionnel à la vitesse de transfert de masse $\beta$ et la différence de densité de vapeur $\rho_\text{v}$ à la surface de la peau et dans l’air :
$$ \dot{m}_{\text{v}} = \beta \times (\rho_\text{v sk}-\rho_\text{v a}) = \beta \frac{M_\text{v}}{RT} (p_\text{sk}-p_\text{a}) \text{ [kg/(m$^2$.s)]} $$
Où $M_\text{v} = 18$ [g/mol] est la masse molaire de la vapeur d’eau, $R = 8,32$ [J/(mol.K)] étant la constante des gaz parfaits.
La puissance échangée par transfert de vapeur sur la peau nue vaut alors, avec $\rho_{\text{a}}$ la masse volumique de l’air :
$$ E = L_{\text{v}} \frac{h_{\text{c}}}{\rho_{\text{a}} c_{\text{a}} Le^{2/3}} \frac{M_\text{v}}{R T}(p_\text{sk}-p_\text{a}) \text{ [W/m$^2$]} $$
Dans cette configuration, il est pratique de disposer d’une relation simple entre le coefficient d’échange convectif et le transfert de masse lié au gradient de pression de vapeur. On pose alors la relation deLewis $LR$ telle que :
$$ LR =\frac{L_{\text{v}}}{\rho_{\text{a}} c_{\text{a}} Le^{\frac{2}{3}} } \frac{M_\text{v}}{RT} = \frac{L_{\text{v}}}{\rho_{\text{a}} c_{\text{a}}} \frac{D^{\frac{2}{3}}}{\alpha ^{\frac{2}{3}}} \times \frac{M_\text{v}}{RT} $$
L’expression de la puissance échangée par transfert de vapeur d’eau $E$ devient par suite :
$$ E = LR \times h_{\text{c}} \times (p_\text{sk}-p_{\text{a}}) \text{ [W/m$^2$]} $$
À température ambiante une valeur couramment acceptée du nombre de Lewis à la surface de la peau est $Le = 0.83$. La diffusivité massique $D$ est calculée avec la relation suivante :
$$ D = D_0 \times \bigg(\frac{T_\text{sk}+273,15}{T_0} \bigg)^{1,81} \times \frac{p_\text{atm}}{p_0} \text{ [m$^2$/s]}, $$
$$ D_0 = 2,26 \times 10^{-5} \text{ [m$^2$/s]}, $$
$$ T_0 = 273,15 \text{ [K]}, $$
$$ p_0 = 101325 \text{ [Pa]}. $$
Une valeur typique pour $D$ à 20°C est :
$$ D = 2,26 \times 10^{-5} \times \frac{293,15}{273,15} = 2,425 \times 10^{-5} \text{[m$^2$/s]} $$
Un facteur de correction $K$ est appliqué pour compenser le gradient de pression de vapeur d’air sec allant en sens inverse du gradient de pression de vapeur d’eau, c’est-à-dire que l’air sec diffuse également vers la surface de la peau [Fobelets,1988]12. Le facteur $K$ se calcule comme suit (pour plus de détails voir [ASHRAE, Chapter 6]13) :
$$ K = \rho_\text{a} \times \frac{p_0}{p_\text{atm}} \times \frac{\ln(\rho_\text{a} / \rho_\text{v})}{\rho_\text{a} - \rho_\text{v}} \text{ [kg/m}^3\text{]} $$
Pour une température de peau de 35 °C / 100% d’humidité et de l’air à 25°C / 50 % d’humidité, ce facteur vaut $K=1,04$. Dans ces conditions, on obtient $LR = 17,4 \times 10 ^{-3}$[K/Pa].
Transfert évaporatif
Lorsque $E_\text{max}$ est connu, on calcule la puissance échangée par sudation :
$$ E_\text{sw} = L_{\text{v}} \times \dot{m}_\text{sw} $$
Où $L_{\text{v}}$ est la chaleur latente de vaporisation et $\dot{m}_\text{sw}$ est le débit de sudation (détaillé dans la section suivante).
On introduit alors la mouillure cutanée de sudation $\omega_\text{sw}$ qui peut être vue comme la raction équivalente de peau mouillée permettant d’atteindre le niveau d’évaporation requis. Elle est définie par le rapport de la puissance évaporée par sudation à la surface de la peau $E_\text{sw}$ et de la puissance maximum d’évaporation :
$$ \omega_\text{sw} = \frac{E_\text{sw}} {E_\text{max}} $$
Le phénomène de diffusion à travers les tissus est également pris en compte. Dans le modèle de Pierce, on considère que 6% de la mouillure cutanée totale $\omega$ sont dus à la diffusion :
$$ \omega = 0,06 + 0,94 \times \omega_\text{sw} $$
La quantité d’énergie perdue par diffusion $E_{\text{d}}$ est définie par :
$$ E_{\text{d}} = \omega E_\text{max} - E_\text{sw} $$
On calcule alors les échanges latents totaux $E$ à la surface de la peau comme la somme des pertes par diffusion et sudation :
$$ E = E_\text{sw} + E_\text{d} $$
De surcroît la mouillure critique, qui détermine la surface de peau pour laquelle l’efficacité de la régulation par sudation et perspiration chute, est déterminée en fonction de la vitesse d’air :
$$ \omega_c = 0,59 \times v^{-0,08} $$
Lorsque la mouillure est supérieure à la mouillure critique la sudation ne peut plus être évaporée entièrement et des gouttes se forment. la mouillure cutanée est alors plafonnée à $\omega = \omega_c$ et on calcule les échanges latent comme :
$$ \omega_\text{sw} = \omega_c / 0,94 $$
$$ E_\text{sw} = \omega_\text{sw} E_\text{max} $$
Les échanges par diffusion sont toujours considérés comme occupant 6% de la surface de la peau :
$$ E_\text{d} = 0,06 \times (1-\omega_\text{sw}) E_\text{max} $$
L’échange latent $E$ peut alors être recalculé (5 équation plus haut).
Régulation de température du métabolisme
Dans le modèle de Pierce, le métabolisme est un système régulé autour des températures de consigne du noyau $T_\text{c}^\text{set}$ et de la peau $T_\text{sk}^\text{set}$. Différentes actions de régulation permettent de maintenir le corps en température ou d’éviter qu’il ne s’échauffe.
Vasomotricité
La variation du débit sanguin volumique $q_{\text{b}}$ [L/(m².h)] est décrite en fonction de l’écart des températures de noyau et de peau avec leurs valeurs de consigne respectives :
$$ q_\text{b}= \frac{q_\text{b}^\text{set}+ C_\text{d} (T_\text{c} - T_\text{c}^{\text{set}})}{1 +C_{\text{s}}(T_\text{sk}^{\text{set}} - T_\text{sk}) }) \mathrm{ [L/(m^2.h)]} $$
Où les constantes de dilatation et de striction valent $C_\text{d} = 200$ [L/(m².h.K)] et $C_\text{s} = 0.5$ [-]. Les températures de consigne du noyau et de peau valent respectivement $T_\text{c}^{\text{set}}=36.8$ [°C] et $T_{\text{sk}}^{\text{set}}=34$ [°C]. Le débit sanguin est compris entre un minimum de 0.5 [L/(m².h.K)] et un maximum de 90 [L/(m².h.K)].
Si les écarts de température de l’équation ci-dessus deviennent négatifs, leur valeur est assignée à zéro afin d’éviter un fonctionnement incohérent de la régulation de température. Par exemple : une action de vasoconstriction lorsque la température de peau est supérieure à la consigne alors qu’au contraire il faudrait augmenter le débit sanguin afin de réduire l’écart à la consigne.
On relève une grande disparité entre les valeurs de constantes de dilatation dans la littérature : ainsi [Hoeppe, 1993]14 propose $C_\text{d}=75$ [L/(m².h.K)] tandis que [ASHRAE_2014] donne $C_\text{d}=12$ [L/(m².h.K)] et [Doherty Arens, 1988] proposent $C_\text{d}=200$ [L/(m².h.K)]. Ceci illustre la variabilité présente dans la nature, dont l’influence est bordée dans les sections suivantes.
Sudation
La sudation est déclenchée en fonction de la température corporelle globale $T_{\text{b}}$, qui est une moyenne des températures de noyau et de peau pondérée par la fraction massique de la peau $\alpha$ :
$$ T_{\text{b}} = \alpha T_\text{sk} + (1-\alpha) T_{\text{c}} $$
où $\alpha$ dépend du débit sanguin qui modifie la masse du cylindre extérieur [Gagge, 1986] :
$$ \alpha = \frac{0,0417737 + 0,7451832 }{q_\text{b} + 0,585417} \text{ [-]} $$
Le débit de sudation est alors décrit en fonction de l’écart à la consigne des températures de corps et de peau :
$$ \dot{m}_\text{sw} = C_\text{sw} \times (T_\text{b} - T_\text{b}^\text{set}) \times e^{ \frac{(T_\text{sk} - T_\text{sk}^{\text{set}})}{10,7}} \text{ [kg/(m$^2$.h)]} $$
Avec $C_\text{sw}=0,170$ [kg/(m².h.K)] d’après [Gagge, 1986] . La température de consigne corporelle est définie telle que $T_{\text{b}}^\text{set} = 0,1 \times T_\text{sk}^\text{set} + 0,9 \times T_\text{b}^\text{set} = 36,49$°C.
Lorsque les écarts de température de l’équation ci-dessus deviennent négatifs, ils sont mis à zéro pour empêcher la sudation lorsque les températures corporelles sont en dessous de leur consigne, c’est-à-dire quand le corps ou la peau sont plus froids que leur température de consigne
Tremblement
Lorsque l’environnement est froid, la réaction physiologique de tremblement permet la génération de chaleur par contraction des muscles. Dans le modèle de Pierce, cela correspond à l’addition d’un terme source $M_\text{sh}$ qui s’ajoute à l’activité métabolique $M$, défini tel que :
$$ M_\text{sh} = C_\text{sh} \times (T_\text{sk}^{\text{set}} - T_\text{sk}) (T_\text{c}^{\text{set}} - T_\text{c}) $$
Le coefficient de tremblement est de $C_\text{sh} = 19,4$ [W/(m².K²)]. Les écarts de température sont considérés comme nuls lorsqu’ils deviennent négatifs. Une formule différente prenant en compte es effets du pourcentage de graisse peut également être appliquée [ASHRAE]15 .
Calcul de la SET (Standard Effective Temperature)
La Standard Effective Temperature (SET) est un indicateur tiré du modèle de Pierce qui sert à quantifier le niveau de confort d’un environnement réel à partir des réactions physiologiques d’un individu. Il s’agit d’une température opérative.
Dans un premier temps, on utilise le modèle de Pierce pour calculer la température de peau $T_\text{sk}$ et la mouillure cutanée $\omega$ résultant de l’exposition d’un individu à l’environnement réel. Le calcul est réalisé pour une durée d’exposition de 60 minutes avec un pas de temps d’intégration d’une minute. La température de peau et la mouillure cutanée obtenues sont alors stockées.
L’individu est ensuite mis dans un environnement de référence aux conditions ambiantes maîtrisées et on détermine la SET, température opérative de cet environnement qui produirait les mêmes réactions physiologiques ($T_\text{sk},\omega$) que l’environnement réel.
L’environnement de référence correspond à une ambiance intérieure de bureau et est défini avec :
- un coefficient d’échange convectif faible, lié uniquement à l’activité du sujet,
- une vêture standardisée, adaptée au niveau d’activité métabolique,
- $\varphi = 50$ % d’humidité relative, ce qui influe sur la pression $p_{\text{a}}$ de vapeur de l’ambiance de référence,
- la température radiante est égale à la température d’air : il s’agit de la SET qui est l’indicateur recherché, à calculer en fonction de la température de peau et de la mouillure cutanée obtenues en environnement réel.
Le coefficient d’échange convectif $h_{\text{c}}$ est défini en fonction du métabolisme tel que :
$$ h_{\text{c}} =3\text{ pour } met < 0,85 $$
$$ h_{\text{c}}=5,66\times(met -0,85)^{0,39}\text{ pour } met \ge 0,85 $$
La vêture est adaptée au niveau d’activité métabolique en met de sorte que :
$$ i_\text{clo}=\frac{1,52}{\frac{M}{58,2} + 0,6944} - 0,1835 \text{ [clo]} $$
Les flux échangés avec l’environnement sont alors recalculés selon les définitions données dans les sections précédentes en tenant compte des changements opérés dans les résistances de vêture $R_\text{cl}$, $R_{\text{e}}$ et dans le coefficient de transfert convectif $h_{\text{c}}$. La SET est obtenue en résolvant l’équation non-linéaire suivante, où $T_\text{sk}$ et $\omega$ sont les réactions physiologiques calculées dans l’environnement réel :
$$ C + R + E = \frac{1}{R_{\text{g}} + R_\text{cl}} \times (T_\text{sk} - SET^* ) + \frac{\omega }{R_{\text{e}}}\times \Big (p_\text{sk} - 50 \% p_\text{vs}(SET^*) \Big) $$
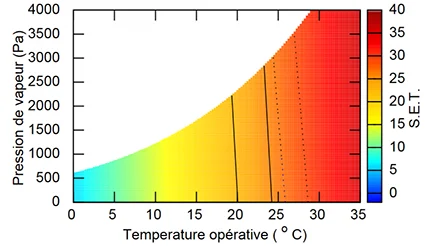
La représentation de la SET en fonction de l’humidité et de la température est donnée sur la Figure 8. On remarque que la dépendance du confort à l’humidité : à température opérative égale, la SET est plus grande pour les humidité élevées que basses. La plage de SET confortable a été déterminée en confrontant le modèle avec une campagne expérimentale et va de 22,2°C à 25,6°C [Nishi, 1977]5.
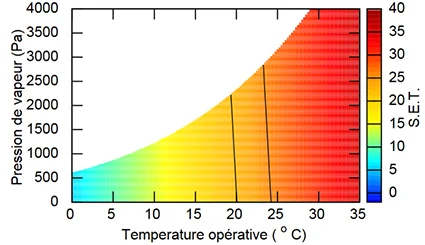
Effet de l’environnement sur le confort
Les espaces semi-ouverts sont soumis à des fortes variations des conditions ambiantes, notamment de vitesse d’air et de température moyenne rayonnante. On s’intéresse donc dans cette partie à leurs effets sur les réactions physiologiques simulées.
Vitesses d’air et propriétés de vêture
La résistance thermique et à la perméation de vapeur sont en réalité affectées par les effets de “pompage” liés au déplacement du porteur, qui favorisent l’admission d’air dans les vêtements, et par les mouvements d’air liés au vent. Leur propriétés convectives s’en trouvent amoindries, de même que leur résistance au transfert de vapeur d’eau. Les paragraphes qui suivent décrivent le calcul de la diminution de ces résistances conformément à la norme ISO 9920 dont la genèse est exposée dans [Holmer, 1999] et [Havenith, 1999] .
Variation de la résistance thermique
La diminution de la résistance au transfert de chaleur est définie dans [Holmer, 1999] . Pour une vitesse de marche inférieure à $v_{\text{w}} < 0,7$ [m/s] (soit 2,5 [km/h]) on définit une: vitesse de marche équivalente \(v_{\text{w}}\) en fonction du niveau d’activité $M$ :
$$ v_{\text{w}} = 0,0052 \times (M - 58) $$
Pour le calcul du coefficient convectif $h_{\text{c}}$ on utilise la vitesse corrigée $v_{\text{c}}$ qui prend en compte la vitesse d’air $v$ et la vitesse de marche $v_{\text{w}}$ :
$$ v_{\text{c}} = \sqrt{ v^2 + v_{\text{w}} ^2} $$
La correction de l’isolation thermique totale convective et de vêture $R_{\text{T}}= R_{\text{g}} + R_\text{cl}$, valide entre 0,2 et 3 [m/s] et $clo \ge 0,6$ est fournie d’après la corrélation :
$$ \frac{R_{\text{T}}^{c}}{R_{\text{T}}} = \exp \left( 0,043 - 0,398 \times v_{\text{c}} + 0,066\times v_{\text{c}}^2 - 0,378 \times v_{\text{w}} + 0,094 \times v_{\text{w}}^2 \right) $$
Où $R_{\text{T}}$ est l’isolation thermique de la vêture et de la couche d’air ambiant, avec pour valeur de résistance thermique de vêture à vitesse d’air nulle $R_\text{cl}$. La résistance convective est calculée pour $v \sim 0$ [m/s].
Une illustration du rapport $R_{\text{T}}^{c}/R_{\text{T}}$ est donnée sur la Fig. 9 en fonction des vitesses d’air et de marche. On constate qu’une vitesse d’air de $\sim 1$ [m/s] à vitesse de marche nulle entraîne une réduction significative de $\sim 25 \%$ de la résistance au transfert thermique. Il importe donc de recalculer le transfert de chaleur en tenant compte de cette diminution afin d’obtenir un bilan thermique au plus juste.
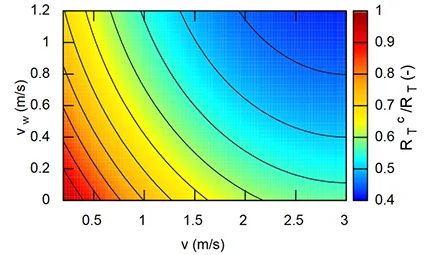
Variation de la résistance à la perméation de vapeur
La perméabilité au transfert de vapeur corrigée $i_{\text{m}}^c$ est donnée par [Havenith, 1999] :
$$ \frac{i_{\text{m}}^{c}}{i_{\text{m}}} = 4,9 - 6,5 \Big( \frac{R_{\text{T}}^{c}}{R_{\text{T}}} \Big) + 2,6 \Big ( \frac{R_{\text{T}}^{c}}{R_{\text{T}}} \Big)^2 $$
La variation de l’indice de perméabilité $i_{\text{m}}$ en fonction de $\frac{R_{\text{T}}^{c}}{R_{\text{T}}}$ est tracée sur la Fig. 10. On voit sur cette illustration que pour une réduction du transfert de chaleur de 70%, la perméabilité à la vapeur $i_{\text{m}}^c$ est multipliée par $\sim 1,6$ par rapport à $i_{\text{m}}$ en ambiance calme. L’équation donnant la résistance au transfert de vapeur $R_{\text{e}}$ s’en trouve modifiée et impacte considérablement le bilan d’énergie latente.
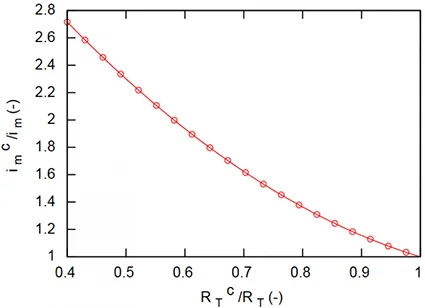
La Fig. 11 montre l’écart entre SET calculée avec des propriétés de vêture constantes (ligne continue) et variables (pointillés) calculées avec les équations précédentes pour une vitesse d’air de $v=1$ [m/s]. Un décalage de la zone de confort vers les températures plus élevées se produit : les propriétés de vêture étant réduites, les transferts sensibles et latents sont augmentés et la température opérative doit être plus élevée afin d’obtenir le même flux perdu à la surface de la peau.
Influence de la température moyenne rayonnante
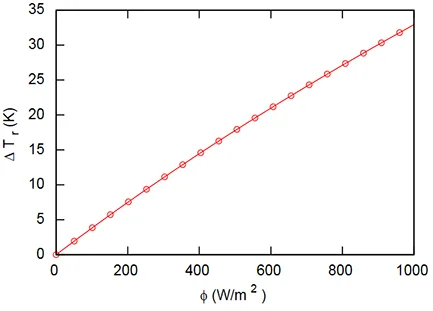
L’équation finale de la partie Echanges Radiatifs donne l’incrément de température moyenne rayonnante $\Delta T_{\text{r}}$ en fonction du flux solaire incident sur l’individu. Ainsi pour 600 [W/m²] de flux incident, on observe un incrément de $\sim 26$ [K] par rapport à la température rayonnante sans ensoleillement.
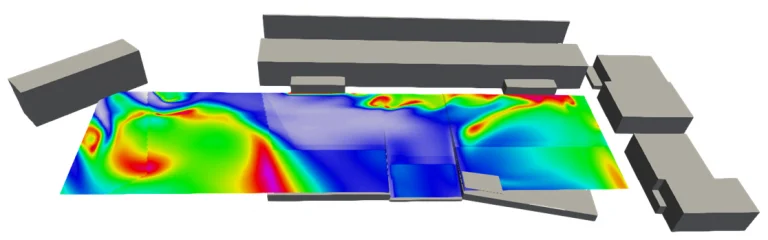
Une illustration de l’influence de la température moyenne rayonnante et de la vitesse d’air est donnée sur la Fig. 13, où l’indicateur de confort SET est donné de manière spatiale. La température rayonnante est calculée à partir des températures de sol et du flux solaire incident. Pour cet exemple, les vitesses d’air ont été calculées par la mécanique des fluides numériques. On a supposé que la température d’air et l’humidité ne sont pas affectées par l’environnement urbain. La disparité de la SET montre l’effet important des vitesses d’air et des températures moyennes rayonnantes.
Influence de la variabilité physiologique sur la SET
On a vu dans les sections précédentes que la SET se calcule à partir des réactions physiologiques d’un individu. Dans la norme [ASHRAE, 2013] , ces réactions sont celles d’un individu masculin. Les paramètres morphologiques étant ajustables, il est envisageable d’utiliser le modèle pour d’autres phénotypes et d’évaluer le confort résultant de leurs réactions physiologiques.
Le modèle de régulation du métabolisme présenté possède un nombre important de paramètres. Afin de montrer la sensibilité du modèle à ceux-ci, on présente ici les effets de la variabilité des paramètres physiologiques sur l’indicateur de confort SET évaluée à partir de tirages aléatoires. La dispersion des résultats sera évaluée en termes d’écart-type : on gardera à l’esprit que $\pm 2$ écarts-types autour d’une valeur moyenne correspondent à 95% de population évaluée.
Présentations des paramètres physiologiques variables
Nombre de caractéristiques physiologiques peuvent être fidèlement représentées par des distributions statistiques gaussiennes (e.g. la taille, la masse). En faisant l’hypothèse que ceci est le cas également pour d’autres paramètres du modèle, la méthode de Monte-Carlo a été utilisée pour évaluer la dispersion de la SET résultant de la variabilité physiologique.
Les paramètres variables choisis pour l’évaluation de la variabilité sont les suivants :
- la taille, la masse et le pourcentage de masse graisseuse,
- les coefficients $C_\text{d}$, $C_\text{s}$, $C_\text{sw}$, $C_\text{sh}$ respectivement pour la dilatation, la striction la sudation et le tremblement,
- la conductance des tissus $U_\text{sk}$ et le débit sanguin basal $q_\text{b}^\text{set}$,
- les températures de consigne de noyau et de peau $T_\text{c}^\text{set}$, $T_\text{sk}^\text{set}$.
La dispersion autour de la masse et de la taille ont été choisies à partir de données issues de l’INSEE. La valeur moyenne des autres paramètres est celle du code original. Pour les températures de consigne de la peau et du noyau, l’écart-type est considéré égal à 0.5% de la valeur moyenne afin de respecter les valeurs minimum et maximum de température interne relevées par [Mackowiak, 1992]16.
Pour les autres paramètres, l’écart-type est pris à 5% de la valeur moyenne, ce qui est une hypothèse conservatrice si l’on considère les disparités observées par exemple pour la constante de dilatation. La conductance des tissus peut également varier dans des proportions plus importantes [Schweiker, 2017]17. La table ci dessous donne le résumé des valeurs numériques utilisées.
Paramètres considérés comme variables dans le modèle de Pierce :
| Paramètre | Valeur moyenne $\mu$ | Écart-type $\sigma$ |
|---|---|---|
| Taille [m] | 1,75 | 0,065 |
| Masse [kg] | 71,4 | 8,9 |
| Graisse [%] | 23 | 7,5 |
| $C_{\text{d}}$ [L/m².h.k] | 200 | 10 |
| $C_{\text{s}}$ [1/K] | 0,5 | 0,025 |
| $C_{\text{sw}}$ [kg/(m².h.K)] | 170 | 8,5 |
| $C_{\text{sh}}$ [kg/(m².K)] | 19,4 | 0,97 |
| $U_{\text{sk}}$ [W/(m².K)] | 5,28 | 0,264 |
| $q_{\text{b}}^{\text{set}}$ [L/(m².h)] | 6,3 | 0,315 |
| $T_{\text{sk}}^{\text{set}}$ [°C] | 33,7 | 0,169 |
| $T_{\text{c}}^{\text{set}}$ [°C] | 36,8 | 0,184 |
Les différences de SET qui en résultent sont présentés dans les sections qui suivent.
Effet du genre
La différence de température de confort entre femmes et hommes a été étudiée de manière expérimentale et numérique [Kingma, 2015]18 [Hoof, 2008]19. On calcule ici la SET moyenne pour les individus masculins et féminins à partir de tirages aléatoires sur les paramètres suivant des lois gaussiennes décrits en section 5.1. Le métabolisme basal est calculé selon la toute première équation en fonction de la taille et de la masse de chaque individu et le niveau de vêture choisi est de 1 [clo].
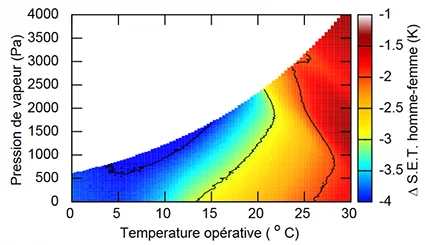
La différence de SET moyenne entre les deux genres est présentée sur la Fig. 14 pour des conditions opératives, soit $T_{\text{a}} = T_{\text{r}}$, à vitesse d’air faible de $v=0,1$ [m/s]. L’écart entre SET moyennes varie entre -4 à -1.25 [K] pour les conditions étudiées.
Dans la plage entre 19 et 25°C de température opérative qui contient la zone de confort définie selon [Nishi, 1977]5 – voir Fig. 8 – l’écart moyen entre genres varie de -3,5 à -2 [K]. Les SET moyennes calculées pour les hommes et les femmes diffèrent donc significativement et dans certains cas cet écart est plus étendu que la zone de confort, qui vaut 3,4 [K].
On remarque de surcroît que d’après les résultats du modèle, la SET obtenue pour les femmes est plus élevée que celle des hommes : ceci implique qu’il faut une température opérative de l’environnement de référence plus élevée pour provoquer la même réaction physiologique que chez les hommes.
Effet de l’environnement
Dans cette section, on présente l’effet de la variabilité d’une population comprenant les deux sexes distribués de manière équiprobable. Les paramètres physiologiques sont distribués selon des gaussiennes comme décrit ici . La vêture est de 1 [clo] et l’activité de 1 [met].
L’écart-type des distributions de SET obtenues en tout point du diagramme psychrométrique est tracé pour conditions de fort vent ($v$=1 [m/s]) sur la Fig. 15. On observe que l’écart-type peut varier de $\sim$ 0,4 à 2 [K]. Ceci implique que dans ces conditions, la température ressentie par 95% de la population varie entre 1,6 et 8 [K], soit quatre écarts-types.
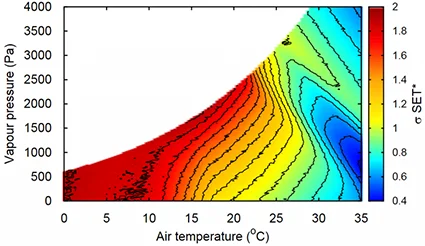
L’écart-type obtenu pour des conditions de flux solaire important, soit $T_{\text{r}}=T_{\text{a}} + 30$, et une vitesse d’air faible $v$=0,1 [m/s] sont représentées Fig. 16. On observe qu’il varie entre $\sim$ 0,2 et 1,4 [K], ce qui implique que 95% de la population se trouve dans une plage variant entre 0,8 et 5,6 [K] en conditions de température radiante élevée.
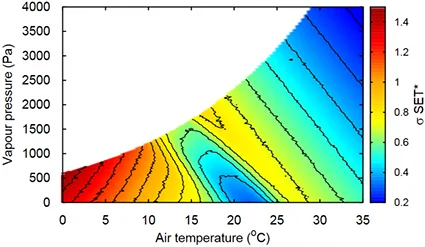
Si ces plages peuvent paraître étendues, la revue bibliographique de [Hoof, 2008]19 mentionne des campagnes expérimentales où des écarts de $\sim 10$ [K] ont été relevés entre température déclarées confortables. En espace intérieur, il apparaît donc ardu de définir une température de consigne adaptée à chacun. En espace extérieur, il convient d’intégrer la variabilité dans l’estimation du confort, dans l’esprit de [Bruse, 2007]20.
Conclusion
Nous avons vu que la détermination du confort dans des ambiances aux conditions variables requiert un indicateur adapté, permettant le calcul des réactions métaboliques en régime transitoire.
La vêture joue également un rôle non négligeable dans le bilan thermique et hydrique du corps humain. Ses propriétés de transfert étant fortement variables avec la vitesse du vent, il est nécessaire d’effectuer un calcul avec la vitesse d’air.
Les caractéristiques morphologiques comme le genre, la masse, la taille ont également une influence notable sur l’évaluation numérique du confort par un modèle de type SET. Une variation importante du confort ressenti peut être introduite par la variabilité physiologique, notamment en conditions extérieures où des vitesses d’air élevées et un fort rayonnement solaire peuvent être rencontrés.
Dans cet article, un modèle dynamique du corps humain pour le calcul du confort a été présenté. D’autres modèles existent et peuvent être utilisés, notamment la Physiological Equivalent Temperature (PET). Celle-ci reprend une grande partie des équations du modèle à deux nœuds présenté ici, ainsi qu’un environnement de référence similaire. La PET est cependant définie comme la température d’un environnement qui provoquerait les mêmes températures de peau et de noyau que l’environnement étudié.
D’autres modèles plus complexes ont été développés, allant jusqu’à 340 noeuds [Fiala, 1999]21 débouchant sur l’indicateur de confort Universal Thermal Comfort Index (UTCI). La complexité du modèle pose cependant des problèmes d’utilisation pratique et de calibrage des informations physiologiques, notamment si l’on souhaite intégrer de la variabilité. Une corrélation basée sur de multiples régressions linéaires en a néanmoins été dérivée et permet d’évaluer le confort d’un piéton marchant à une vitesse de 4 [km/h].
L’historique thermique de l’individu a également une influence sur son ressenti : à titre d’exemple, on apprécie bien une ambiance à 16°C pendant quelques minutes après avoir fait un effort intense, tandis que la même ambiance serait trop jugée froide lorsque le corps est à l’équilibre thermique. L’approche de l’alliesthésie développée par [Parkinson, 2012]22 propose un modèle pour ce phénomène. La notion de “plaisir” ressenti lors de phénomènes alliesthésique dépasse également l’approche usuelle, qui se concentre sur la neutralité thermique.
Les aspects psychologiques du confort ne doivent pas non plus être négligés : il a en effet été prouvé qu’à conditions identiques, le ressenti du confort est meilleur dans une pièce aménagée (mobilier, décoration) que dans une pièce nue [Rohles, 2007]23. De même, l’effet placebo a un impact : lorsque l’utilisateur pense avoir le contrôle sur la température de consigne, son ressenti s’en trouve favorablement impacté, que ce contrôle soit effectif ou non [Rohles, 2007]23.
Dans cette branche, les appoints locaux de confort de type chaufferettes, sièges chauffants, ventilateurs de bureau ou intégrés en assise, apportent une réponse intéressante à la variabilité des températures de confort. De considérables économies d’énergie ont été enregistrées sur un site pilote [Brager, 2015]24 : en fournissant à chaque individu une puissance de l’ordre d’une vingtaine de Watts, la baisse de la température de consigne générale a permis d’observer une réduction de puissance de 500 W/personne.
Le code source des indicateurs SET et PET est téléchargeable dans l’onglet Outils / Scripts / Python du site! Enjoy 😉
Vernon, H. M. (1936), Accidents and their Prevention, DOI ↩︎
Fanger, P. O. (1970), Thermal Comfort: Analysis and applications in environmental engineering, Copenhagen: Danish Technical Press ↩︎ ↩︎
Van Hoof, J. (2008), Forty years of Fanger’s model of thermal comfort: comfort for all?., Indoor air, 18(3), 182-201. ↩︎
Gagge, A. P. (1936). The linearity criterion as applied to partitional calorimetry. American Journal of Physiology-Legacy Content, 116(3), 656-668. ↩︎
Nishi, Y.,& Gagge, A. P. (1977). Effective temperature scale useful for hypo-and hyperbaric environments. Aviation, space, and environmental medicine, 48(2), 97-107. ↩︎ ↩︎ ↩︎
Höppe, P. (2002). Different aspects of assessing indoor and outdoor thermal comfort. Energy and buildings, 34(6), 661-665. DOI ↩︎
Part, V. (2008). I: Environmental meteorology, methods for the human-biometeorological evaluation of climate and air quality for the urban and regional planning at regional level. Part I: Climate. Part I: Climate. VDI/DIN-Handbuch Reinhaltung der Luft, 29. DOI ↩︎
Schiavon, S.,& Lee, K. H. (2013). Dynamic predictive clothing insulation models based on outdoor air and indoor operative temperatures. Building and Environment, 59, 250-260. DOI ↩︎
A.P. Gagge, J.A.J. Stolwijk, Y. Nishi, Effective temperature scale based on a simple model of human physiological regulatory response, ASHRAE Trans. 77 (1971) 247– 263. ↩︎
Cain, J. B., Livingstone, S. D., Nolan, R. W.,& Keefe, A. A. (1990). Respiratory heat loss during work at various ambient temperatures. Respiration physiology, 79(2), 145-150. DOI ↩︎
Helbig, A., Baumüller, J.,& Kerschgens, M. J. (Eds.). (2013). Stadtklima und Luftreinhaltung. Springer-Verlag. ↩︎
Fobelets, A., 1988, Rationalization of the Effective Temperature ET^ as a Measure of the Enthalpy of the Human Indoor Environment*, ASHRAE Transactions ↩︎
ASHRAE, 2009, ASHRAE Handbook, Fundamentals. Chapter 6: Mass transfer ↩︎
Höppe, P. R., 1993, Heat balance modelling. Experientia, 49, 741-746. ↩︎
ASHRAE, 2009, ASHRAE Handbook, Fundamentals. Chapter 9: Thermal Comfort ↩︎
Mackowiak, P. A., Wasserman, S. S.,& Levine, M. M., 1992. A critical appraisal of 98.6 F, the upper limit of the normal body temperature, and other legacies of Carl Reinhold August Wunderlich. Jama, 268(12), 1578-1580. [PDF link] ↩︎
Schweiker, M., Fuchs, X., Becker, S., Shukuya, M., Dovjak, M., Hawighorst, M.,& Kolarik, J. (2017). Challenging the assumptions for thermal sensation scales. Building Research& Information, 45(5), 572-589. [PDF link] ↩︎
Kingma, B.,& van Marken Lichtenbelt, W. (2015). Energy consumption in buildings and female thermal demand. Nature climate change, 5(12), 1054-1056. PDF Link ↩︎
Van Hoof, J. (2008). Forty years of Fanger’s model of thermal comfort: comfort for all?. Indoor air, 18(3), 182-201. PDF Link ↩︎ ↩︎
Bruse, M. (2007, November). Simulating human thermal comfort and resulting usage patterns of urban open spaces with a multi-agent system. In Proceedings of the 24th International Conference on Passive and Low Energy Architecture PLEA (Vol. 24, pp. 699-706). PDF Link ↩︎
Fiala, D., Lomas, K. J.,& Stohrer, M. (1999). A computer model of human thermoregulation for a wide range of environmental conditions: the passive system. Journal of applied physiology, 87(5), 1957-1972. PDF Link ↩︎
Parkinson, T., De Dear, R.,& Candido, C. (2012, April). Perception of Transient Thermal Environments: pleasure and alliesthesia. In Proceedings of 7th Windsor Conference, Windsor, UK (No. 56). PDF Link ↩︎
Rohles, F. (2007). Temperature& Temperament. American Society of Heating, Refrigerating and Air-Conditioning Engineers, 14-19. PDF Link ↩︎ ↩︎
Brager, G., Zhang, H.,& Arens, E. (2015). Evolving opportunities for providing thermal comfort. Building Research& Information, 43(3), 274-287. PDF Link ↩︎