Analyse de sensibilité

Introduction

Certains modèles sont complexes ou ont un grand nombre de paramètres. Dans ces situations il est souvent délicat de déterminer un classement des paramètres les plus influents et de connaître leurs éventuelles interactions. Diverses méthodes existent pour traiter cette question, on s’intéresse ici à l’analyse de sensibilité selon la méthode de Morris .

À titre d’exemple, regardons l’image animée ci-dessous. Elle figure l’effet d’une poussée sur un solide et du déplacement $F$ qui en résulte. En somme on observe le comportement de la fonction $F$, le déplacement, par rapport à un paramètre $X$, la forme. On obtient donc une variation $X\frac{\Delta F}{\Delta X}$, qui est la quantité dont a varié la fonction observée entre deux valeurs du paramètre.

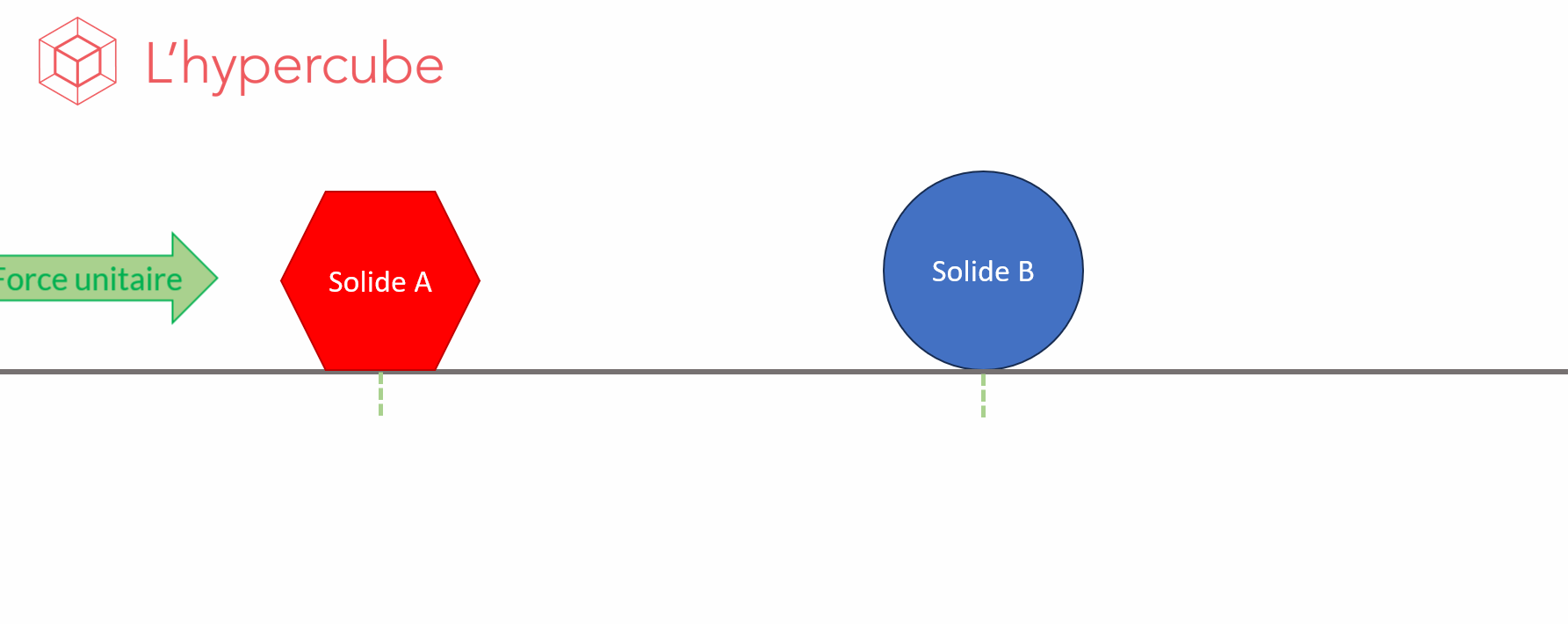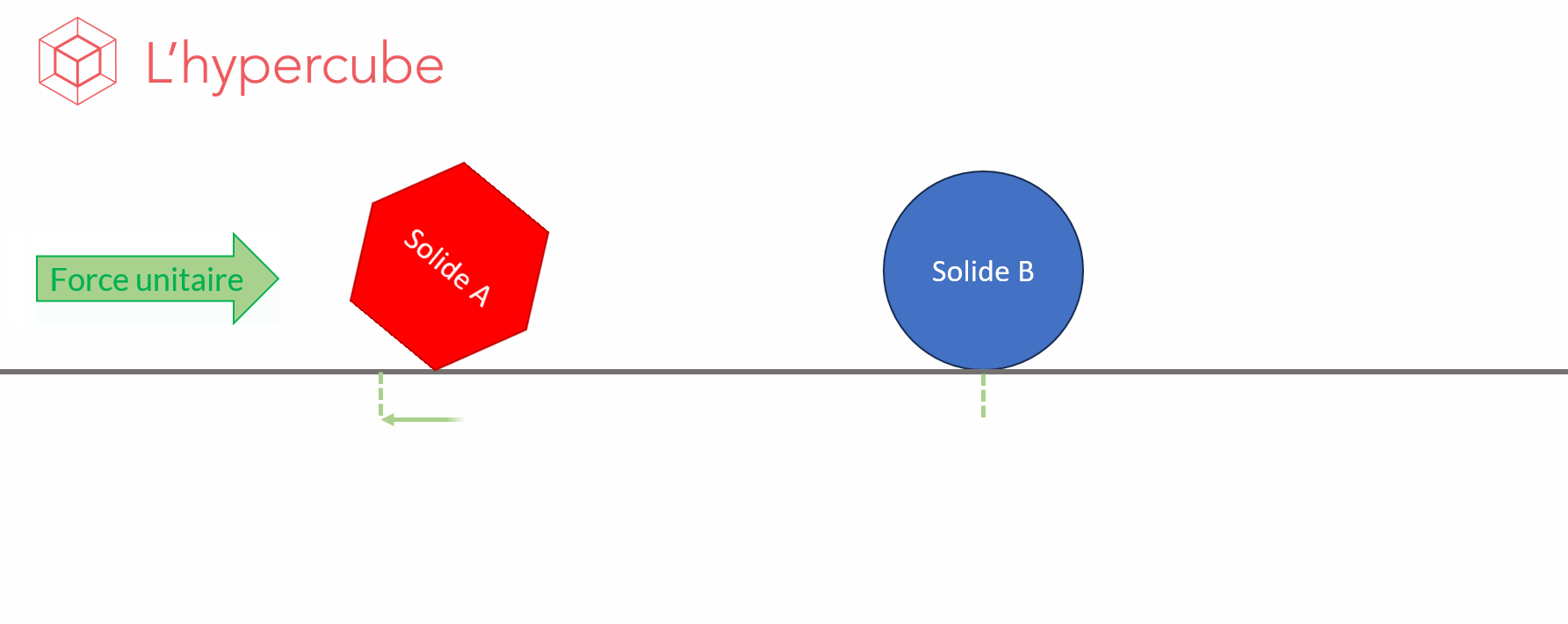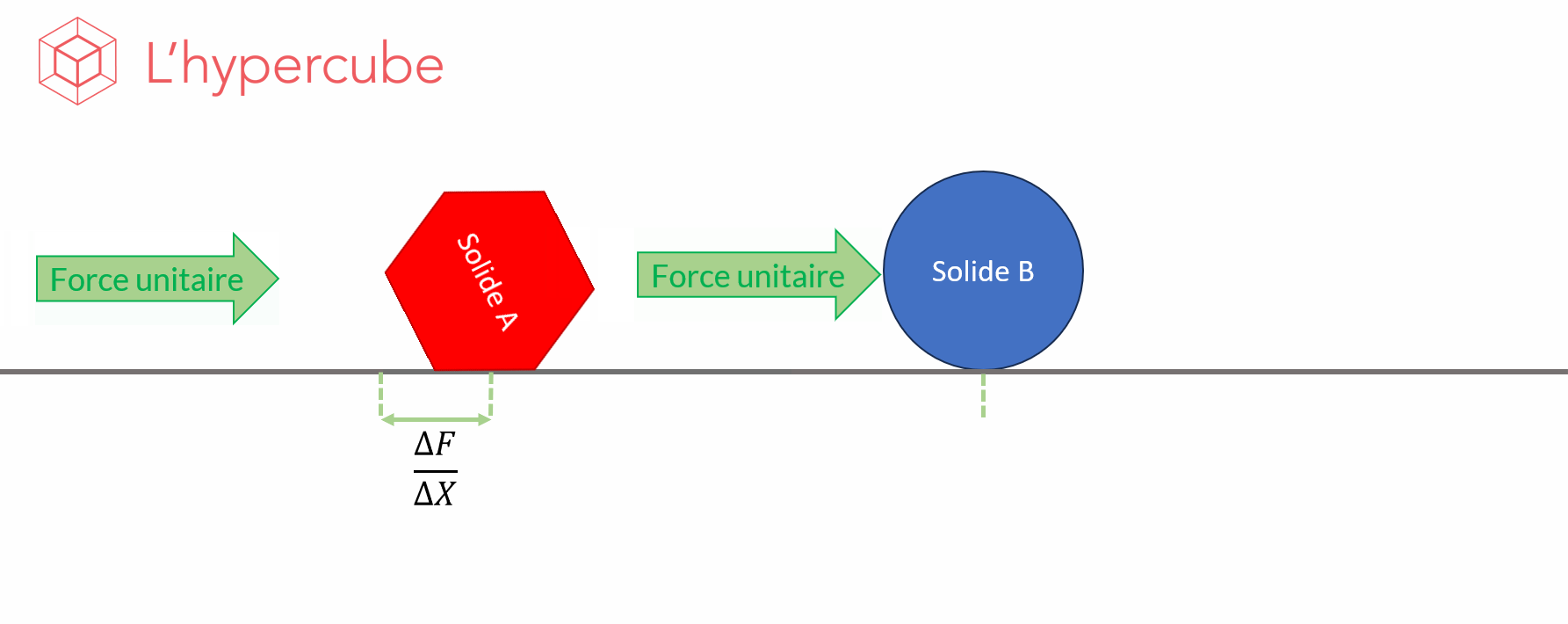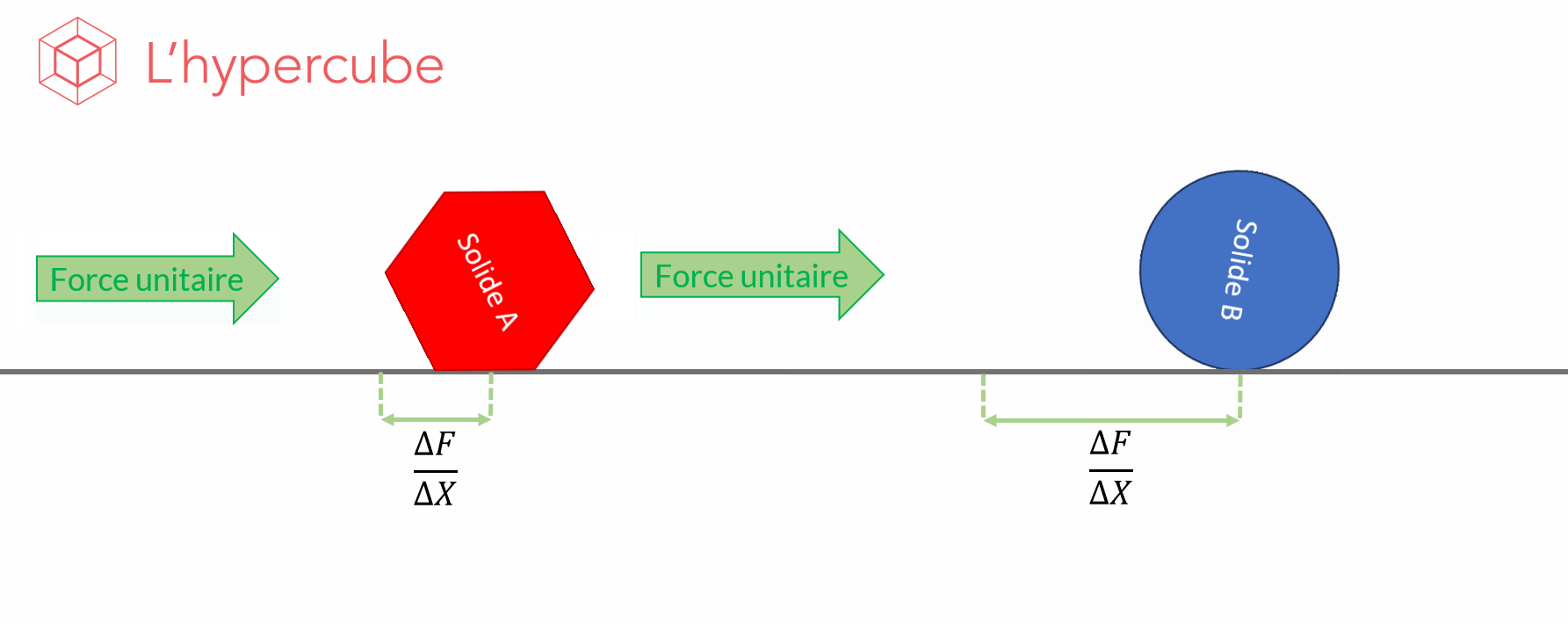
L’idée de l’analyse de sensibilité est d’effectuer suffisamment de simulations afin d’estimer l’effet moyen de la variation d’un paramètre sur la sortie observée.

Principe de la méthode de Morris

Il s’agit d’une méthode d’analyse de sensibilité dite “One at a time”, où un seul paramètre est modifié à chaque simulation. La variation de fonction objectif $F$ par rapport à un paramètre $X_i$ est calculée par différence finie entre deux jeux de paramètres identiques à l’exception d’un seul paramètre : voir la figure ci-dessous où les paramètres sont changés un par un et où on évalue l’effet dit “élémentaire” de chacun.

Ainsi, s’il y a $d$ paramètres, il faut $d$+1 simulations pour évaluer l’effet d’une variation de chacun d’entre eux, soit $\frac{\Delta F}{\Delta X_1},\frac{\Delta F}{\Delta X_2},…,\frac{\Delta F}{\Delta X_d}$.

Afin de calculer un effet élémentaire moyen $\frac{\Delta F}{\Delta X_i}$, on génère à nouveau $d$+1 jeux de paramètres et on répète l’opération un nombre de fois $r$ : il s’agit des “répétitions”.

Au total on aura donc réalisé $n = r \times (d+1)$ simulations. Une valeur communément admise dans la littérature est $r \sim$ 10, soit un nombre total d’évaluation de l’ordre de $n \sim 10 \times d$.

On traite alors la série des effets élémentaires $\frac{\Delta F}{\Delta X_i}$ de chaque paramètre afin de calculer un effet élémentaire moyen $\mu_i$ et un écart-type $\sigma_i$. Pour mémoire, plus l’écart-type d’une série est grand, plus les valeurs sont dispersées autour de la moyenne. À titre d’exemple, la figure i-après représente la variation d’une fonction-objectif par rapport à un paramètre $X_1$.

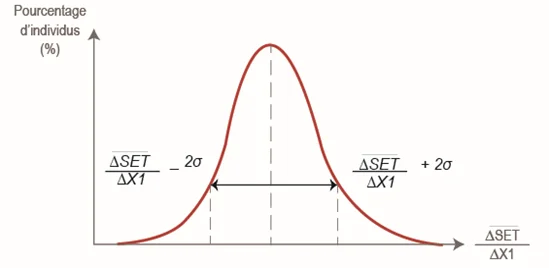
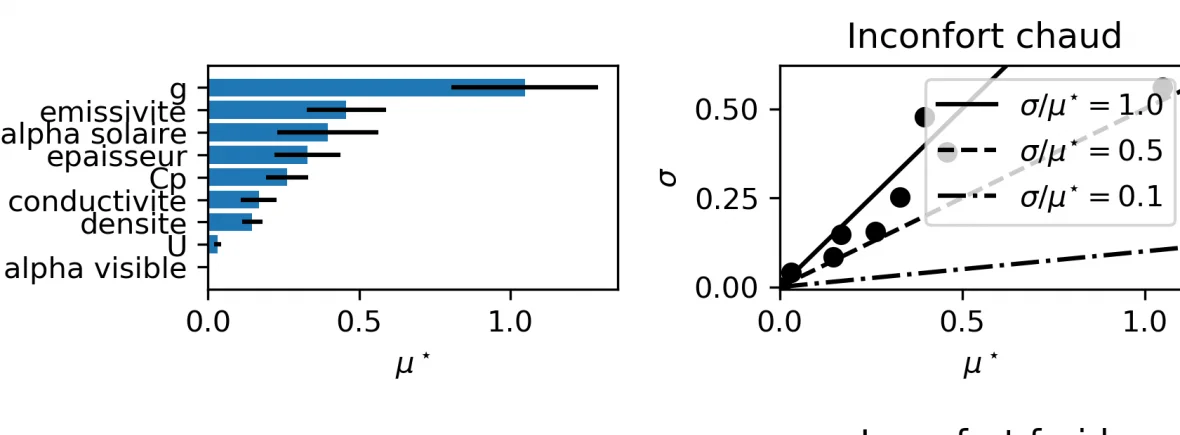
Le classement des paramètres se fait alors en fonction du graphe $(\mu,\sigma)$, tel que présenté ci-dessous. Les paramètres influents ont un effet élémentaire moyen élevé : une variation du paramètre engendrera une variation significative de la fonction objectif. Si l’écart-type de la série des effets élémentaires est faible, on considère que l’effet est linéaire. Si cet écart-type est important, notamment s’il est de l’ordre de grandeur de l’effet élémentaire (autrement dit : supérieur ou égal à la première bissectrice), l’effet est non-linéaire ou provoque des interactions avec d’autres paramètres.

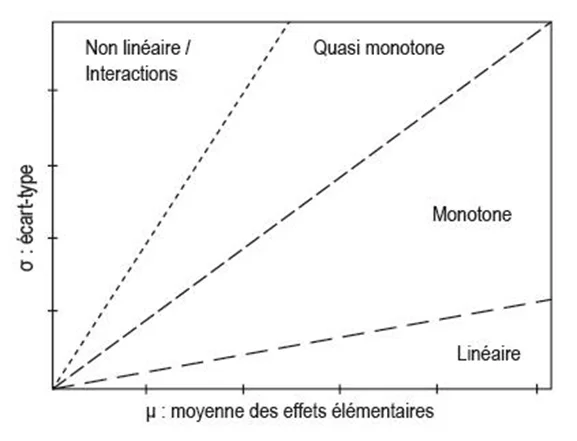
Exemple d’application

Un exemple de résultat appliqué à la thermique des grands volumes est donné dans ce paragraphe.

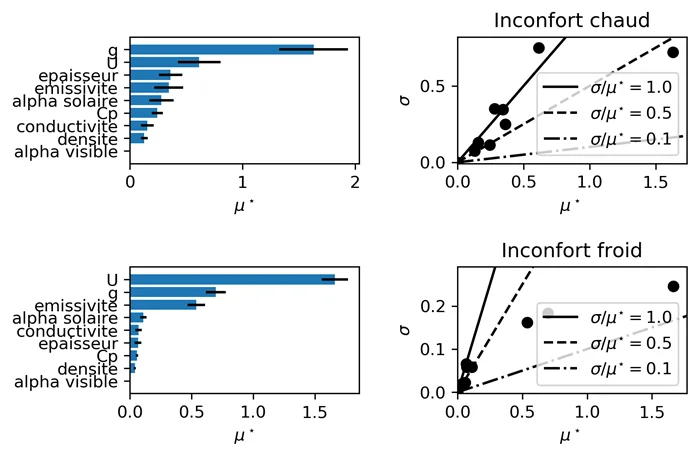
On veut connaître les paramètres les plus influents dans le cadre de la rénovation d’une verrière. Les paramètres choisis sont l’épaisseur, la conductivité, la capacité thermique massique, la densité, l’absorptivité solaire & visible ainsi que l’émissivité de surface de la dalle de sol ; le facteur $g$ et le facteur $U$ du vitrage.

La fonction objectif est la moyenne saisonnière des écarts entre l’indicateur SET à l’instant $t$ et le centre de la plage de SET dite confortable (donc la moyenne de 22,2 et 25,5°C SET). La saison d’hiver et celle d’été sont simulées : on observe que le classement des paramètres n’est pas le même en fonction de la saison. L’ordre de grandeur de l’effet élémentaire moyen est de $\sim$ 1 [K] d’écart à la SET de confort.

lien du package SAlib.