Projection de champs

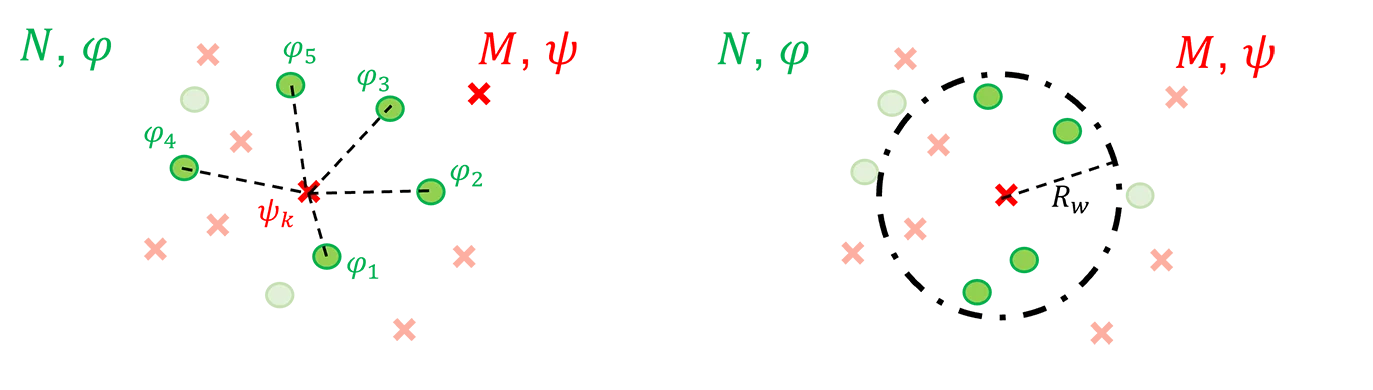
Présentation du problème

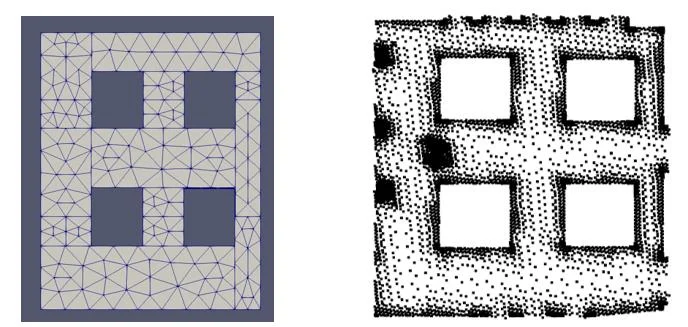
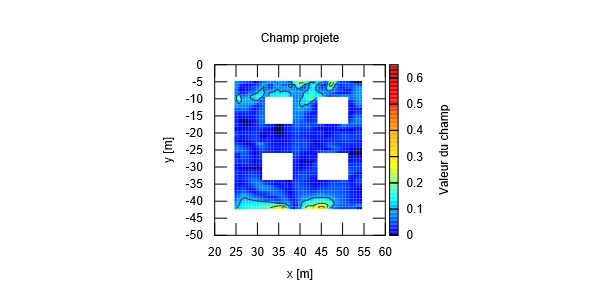
Un écueil courant lors de la résolution de problèmes avec des physiques multiples est que l’utilisation de plusieurs outils entraîne souvent la création de maillages différents (voir la figure ci-dessous). Il s’agit alors de projeter les champs sur une grille commune afin de pouvoir réaliser des calculs en un même point de l’espace pour les deux grandeurs calculées.

Dans la section qui suit, on présente un outil mathématique permettant de projeter un champ sur un autre, régulier au non.

Méthodes de projection

Il existe plusieurs algorithmes de complexité variable pour réaliser une projection de champ. On en présente quelques variantes dans cette section.

Les plus proches voisins

Une technique pour projeter un champ sur l’autre consiste à résoudre un problème de minimisation. On explicite ici la méthode succincte donnée dans code Aster en dimension deux pour l’algorithme des plus proches voisins.

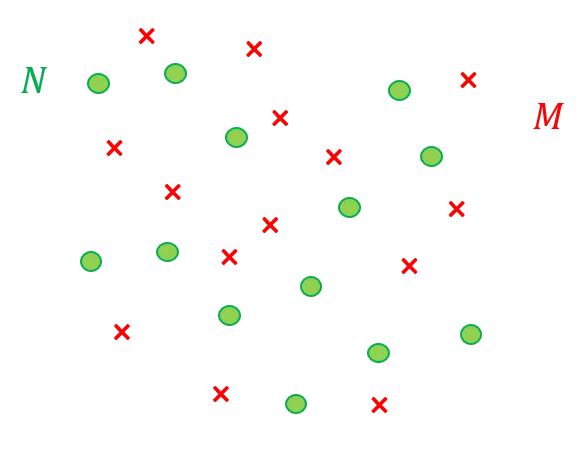
Il s’agit de projeter un nuage de points $N$ portant un champ $\varphi$ sur un ensemble de points $M$ différent de $N$. Appelons $\psi$ la projection de $\varphi$ sur $M$.

Pour chaque point $k$ appartenant à $M$ de coordonnées $(x_k,y_k)$, on cherche ses $n$ plus proches voisins appartenant à $N$, ainsi qu’illustré sur la Figure qui suit.

La valeur du champ sur le point projeté $\psi_k$ est calculée avec les coefficients $a_k$, $b_k$, $c_k$ de sorte que : $$ \psi_k = a_k + b_k x_k + c_k y_k $$

Il s’agit donc de trouver, pour l’ensemble des points $k$ du nuage $M$, les vecteurs $[a_k]$, $[b_k]$, $[c_k]$ des coefficients qui minimisent la distance entre le champ projeté $\psi$ et le champ $\varphi$. Ainsi, pour tout point $k$ du nuage $M$ on cherche à minimiser les moindres carrés $\varepsilon_k$ entre la fonction $\psi_k$ et le champ $\varphi_i$ sur les \(n\) plus proches voisins du point :

$$ \varepsilon_k = \sum_{i=1}^{n} w(d_i) \big(\psi_k-\varphi_i \big)^2 $$

Où la fonction de pondération $w(d_i)$ dépend de la distance $d_i$ entre le point $(x_i,y_i)$ du nuage initial et le point $k$ de la grille de projection $(x_k,y_k)$ :

$$ w(d_i) = \exp^{-(\frac{d_i}{d_{\text{r}}})^\beta} $$

où :

• $d_i$ est la distance $(i-k)$ soit $d_i=\sqrt{(x_i-x_k)^2+(y_i-y_k)^2}$,
• $d_{\text{r}}$ est la distance de référence du maillage. Celle-ci est définie comme le rayon du plus petit cercle centré en un point de $M$ contenant trois points du nuage $N$, comme illustré sur la figure ci-après (on pourra déterminer ce rayon avec un kdtree du package scipy par exemple). En première approximation, si la distance $\Delta x$ entre deux points du nuage est connue (cas d’un maillage régulier par exemple), on peut prendre $d_{\text{r}} \sim \frac{\Delta x}{2}$. utrement, on pourra aussi utiliser la distance $d_{\text{r}} \sim \frac{D^2}{N} = \frac{2D}{\sqrt{N}}$ où $D$ est la distance entre les deux points les plus éloignés du nuage.

Le choix du jeu de paramètres $(n,M,\beta,d_{\text{r}})$ influe sur la performance globale de l’algorithme : selon la distance entre points du maillage il convient d’avoir un nombre de points de projection $M$ suffisants, tout en gardant à l’esprit que la durée de calcul est proportionnelle à $M$. De plus, s’il l’on choisit $\beta>1$, l’influence des points lointains est rapidement amortie lorsque leur distance au point de référence est supérieure à $d_{\text{r}}$.

Les tests menés sur champs analytiques avec un densité de points homogène ont montré cependant que l’augmentation du nombre de voisins n’affecte pas la qualité de la projection. Pour de tels champs l’utilisation de $n \in$ [4;8] est conseillée, avec pour coefficient de fonction de pondération $\beta$=1.5.

La méthode de Shepard

(élaboré à partir des travaux de T. Klinyam au sein d’AREP)

Cette méthode est une forme de pondération inverse à la distance qui est une méthode d’interpolation spatiale. L’effort principal ici va consister à construire une fonction d’interpolation $Q(x,y)$ pour le champ considéré, au lieu d’utiliser directement la valeur du champ.

Sur les champs analytiques étudiés, cette méthode est $\sim 2 \times$ plus performante en termes de précision, pour un temps d’exécution augmentant d’un ordre de grandeur. Si le gain peut paraître faible par rapport au temps de calcul, la robustesse de la méthode de Shepard pour la projection de champs réels a été éprouvée, notamment car elle induit moins de lissage sur ceux-ci.

Construction d’une fonction d’interpolation sur le champ initial \(N\)

La forme la plus simple de la méthode est appelée “Méthode de Shepard” (Shepard 1968) avec l’équation suivante :

$$ f\left(x,y\right)=\sum_{k=1}^{N}{w_k\left(x,y\right) F_k} $$

Où $w_k$ est une fonction de pondération généralement dépendante de la distance et $F_k$ est une fonction qui permet de calculer la valeur au point $k$. Dans les cas les plus simples, comme la méthode des plus proches voisins, on définit $F_k=\varphi_k$, soit la valeur du champ initial au point $k$.

Dans la méthode de Shepard, on définit la pondération telle que :

$$ w_k = \frac{\left[\frac{(R_k - d_k)_{+}}{R_k d_k}\right]^2}{\sum_{k=1}^{N}{\left[\frac{ (R_k-d_k)_{+} }{R_k d_k} \right]^2}} $$

où :

• $d_k$ est la distance entre le point $(x,y)$ et le point $(x_k,y_k)$ soit $d_k = \sqrt{\left(x-x_k \right)^2+\left(y-y_k\right)^2}$​, dont $\left( x,y \right)$ sont les coordonnées du point interpolé et $(x_k,y_k)$ sont des coordonnées du nuage des points du champ de départ,
• $R_{\text{q}}$ est le rayon d’influence d’un cercle centré sur le point $(x,y)$ (représenté sur la figure ci-dessous), en pratique on choisit $N_{\text{q}} \sim$ 40 - 50. Le rayon d’influence est calculé de sorte que :

$$ (R_{\text{q}}-d_k)_{+} = R_{\text{q}} - d_k \text{ pour } d_k < R_{\text{q}} $$

$$ (R_{\text{q}}-d_k)_{+} = 0 \text{ pour } d_k \ge R_{\text{q}} $$

Soit $D$ la distance entre 2 points les plus éloignés du nuage $N$. On définit $R_{\text{q}}$ via le paramètre de fonction nodale $N_{\text{q}}$ tel que :

$$ R_{\text{q}}=\frac{D}{2}\sqrt{\frac{N_{\text{q}}}{N}} $$

Pour ce qui est de la valeur de la fonction $F_k$, on construit ensuite une loi d’interpolation $Q_k(x,y)$ définie de la manière suivante :

$$ Q_k(x,y)=\varphi_k+a_{k2}(x-x_k)+a_{k3}(y-y_k)+a_{k4}(x-x_k)^2 \\ +a_{k5}(x-x_k)(y-y_k)+a_{k6}(y-y_k)^2 $$

Où $\varphi_k$ est la valeur sur le point $(x_k,y_k)$ et les coefficients $(a_{k2}, …,a_{k6})$ sont propres à chaque point $(x_k,y_k)$. On les détermine par la minimisation des moindres carrés suivants, pour $k \in [1,N^{\star}]$, où $N^{\star}$ est le nombre de points dans le rayon d’influence $R_{\text{q}}$ (afin de ne pas surcharger les notations on écrira indifféremment $N^{\star}$ et $N$ dans la suite, en effet la fonction de pondération annule la contribution des autres points du nuage) :

$$ \varepsilon_k = \sum_{ i=1\ et\ i\neq k}^{N^*}\left [ \frac{Q_k(x_i,y_i)-\varphi_i}{\rho_k(x_i,y_i)} \right ]^2 $$

Soit, explicitement :

$$ \varepsilon_k = \sum_{ i=1 \text{ et } i \neq k}^{N^*} \bigg [ \frac{(R_k - d_k)_{+}}{R_k d_k} \cdot \bigg ( \varphi_{k} + a_{k2}(x_i-x_k) + a_{k3}(y_i-y_k) + a_{k4}(x_i-x_k)^2 \\ + a_{k5}(x_i-x_k)(y_i-y_k) + a_{k6}(y_i-y_k)^2 - \varphi_i \bigg ) \bigg ]^2 $$

Avec $d_i$ la distance entre les points $i$ et $j$ : $d_i= \sqrt{(x_k-x_i)^2+(y_k-y_i)^2}$

L’équation d’interpolation devient alors :

$$ f(x,y)=\sum_{k=1}^{N^*}{w_k(x,y) \cdot Q_k(x,y)} $$

On notera que l’effort calculatoire est situé dans l’étape d’identification des paramètres $a_{2k},…, a_{6k}$ : plus le nombre $N_{\text{q}}$ est grand, plus le nombre de points concerné est important, ce qui augmente la quantité de coefficients à déterminer pour la fonction de minimisation.

Calcul de la projection sur le champ $M$

On définit alors le rayon d’influence $R_{\text{w}}$, dont une illustration est donnée sur la Figure ci-après, tel que :

$$ R_{\text{w}}=\frac{D}{2}\cdot \sqrt{\frac{N_{\text{w}}}{N}} $$

En pratique, un choix efficace consiste à prendre $N_{\text{w}}=N_{\text{q}}/2$.

La projection sur le point $(x_m,y_m)$ du nuage $M$ est calculée en faisant la somme des fonctions d’interpolations pour chaque point dans le rayon d’influence $R_{\text{w}}$ (voir figure ci-après) :

$$ \psi_m=\sum_{k=1}^{N}{w_k(x_m,y_m)}\cdot Q_k(x_m,y_m) $$

Il s’agit ensuite de calculer la projection $\psi_m$ avec la fonction de pondération $w_k$ définie plus haut, dont le rayon d’influence $R_{\text{w}}$ est défini deux équations au dessus, en utilisant le paramètre d’influence $N_{\text{w}}$.

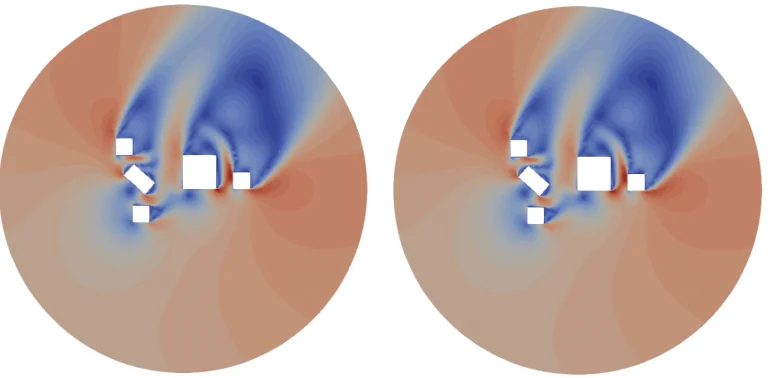
Un exemple d’application de la projection selon la méthode de Shepard est donné ci-dessous.

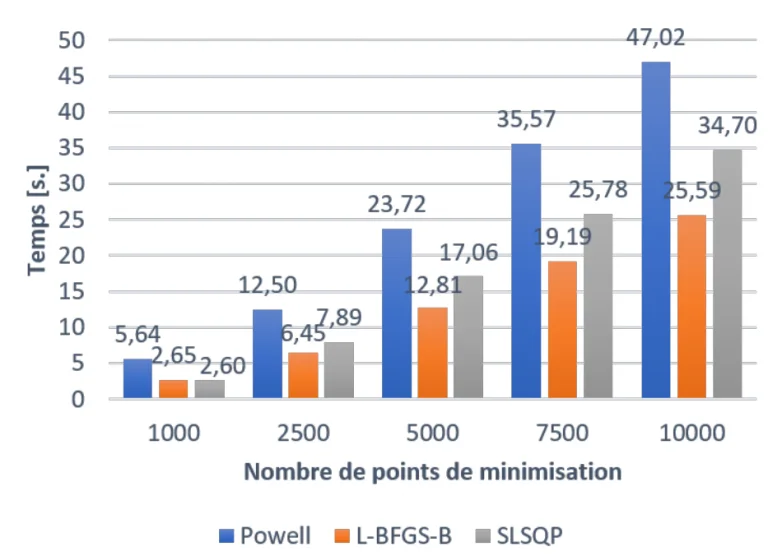
Résultats sur le temps d’exécution des différents algorithmes de minimisation

On compare ici quelques unes des fonctions proposées la librairie optimize de scipy pour un problème de projection de champ analytique en 2D. De manière intéressante, la méthode L-BFGS-B est la plus performante. À partir de plus de 2000 points sur lesquels on calcule la fonction d’interpolation $Q(x,y) $, on constate une augmentation linéaire du temps de calcul.