Qualité d’Air en gares souterraines
Introduction & Constat initial
La qualité d’air dans les gares souterraines est un sujet de préoccupation croissant dans les villes possédant un réseau de transport urbain. En France, des campagnes de mesure en continu et libres d’accès ont lieu à la SNCF ou à la RATP, donnant accès aux données de concentration des $PM_{2.5}$ et $PM_{10}$.
En exploitant les données disponibles, on peut observer la corrélation entre trafic ferroviaire (en traits continus) et la concentration en $PM_{10}$ (pointillés). La figure ci-dessous représente une semaine moyenne dans la gare souterraine de St-Michel Notre-Dame. On peut alors supposer que la quantité d’aérosol en suspension provient en majorité du freinage et de la resuspension.
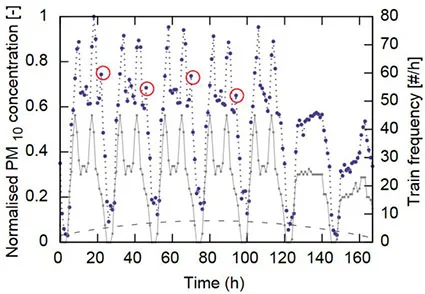
Sur cette figure, on constate d’une part que les maxima de concentration en $PM_{10}$ sont oncomitants avec les pics de de trafic du matin et du soir, d’autre part, les concentrations en fin de semaine diminuent avec le trafic ferroviaire.
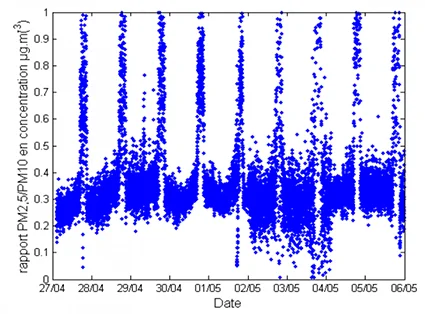
En observant le ratio $PM_{2.5}/PM_{10}$ sur une semaine en gare de Magenta comme présenté sur sur la Figure 2 ci-après issue de [Fortain, 2007] , on constate que celui-ci est compris entre $\sim 0.25$ et $0.35$ dans la journée, tandis qu’il atteint 1 durant la nuit. Les $PM_{2.5}$ étant comprises dans les $PM_{10}$, ceci signifie que les particules les plus grosses disparaissent progressivement de l’aérosol pendant la période nocturne : seules les plus fines subsistent.
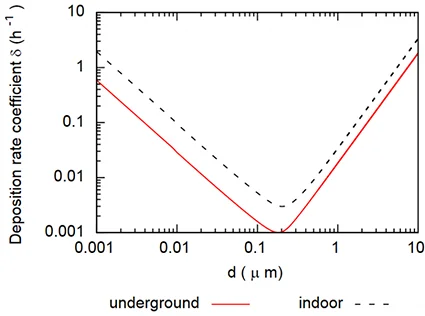
Ce phénomène peut s’expliquer par la vitesse de déposition des particules. En effet, celle-ci est plus importante pour les particules de diamètre important. La Figure 3 qui suit présente le taux de déposition des particules en fonction de leur diamètre d’après [Lai et Nazaroff 2000] . Sans surprise, la déposition gravitaire est prédominante pour les On les particules de diamètre supérieur à 1 [µm]. On notera que les particules les plus fines, de diamètre nférieur à 0.01 [µm] se déposent également de manière plus importante : ceci est lié u mouvement d’agitation brownien qui fait diffuser les particules de très petite taille sur les surfaces. Dans la gamme de diamètres intermédiaire, les particules sont trop grosses pour être soumises au mouvement brownien du gaz dans lequel elles évoluent (l’air) et n’ont pas assez de masse pour une sédimentation gravitaire : les mouvements de convection naturelle de l’air suffisent à les maintenir en suspension.
Ces observations ont donné lieu au développement de modèles successifs de prédiction de la qualité d’air en gare souterraine. Les sections qui suivent exposent la méthode développée dans [Walther et Bogdan 2017a] et [Walther et al. 2017b] , disponibles dans la section Publications](/references/publications/) de ce site.
Mise en équation
En se basant sur le constat précédent et l’hypothèse du mélange homogène, on établit un système différentiel qui considère les concentrations de deux classes de particules $C_a$ pour les $PM_{2.5}$ et $C_b$ pour les $PM_{2.5-10}$, la somme des deux étant égale à la concentration en $PM_{10}$. Ceci permet de capter les dynamiques lentes et plus rapides des particules de l’aérosol :
$$ \frac{d C_a}{dt} = \alpha_a N^2(t) + \tau (C_a^\text{ext}-C_a) - \delta_a C_a $$
$$ \frac{d C_b}{dt} = \alpha_b N^2(t) + \tau (C_b^\text{ext}-C_b) - \delta_b C_b $$
Où $N$ est le nombre de trains par unité de temps, $\alpha_a$, $\alpha_b$ sont les termes d’émission des $PM_{2.5}$ et $PM_{2.5-10}$ et $\delta_a$, $\delta_b$ les taux de déposition calculés d’après la méthode de [Lai et Nazaroff 2000] .
Le taux de renouvellement d’air $\tau$ est décomposé en un taux de ventilation naturelle $\tau_0$ et une ventilation par effet piston $\beta \times N$, où $\beta$ [-] est le volume d’air extérieur entraîné par le départ et l’arrivée du train, divisé par le volume de la gare.
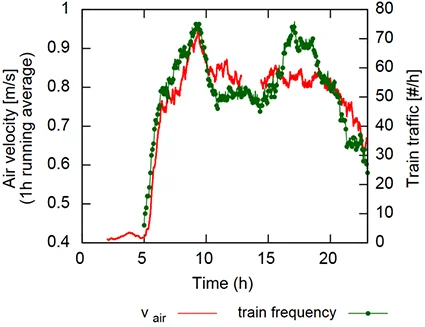
Dans la revue de la littérature par [Nicholson 1988]1, le taux de resuspension suit la vitesses avec une loi puissance avec un exposant allant de 1 à 6. Le terme d’émission apparente $\alpha$ est ainsi supposé varier avec le carré du nombre de trains $N^2$ : en effet, si les trains sont des événements discrets, on considère qu’ils amènent à une augmentation de la vitesse moyenne en gare. La campagne expérimentale de mesure des vitesses d’air menée en gare de St-Michel Notre-Dame en février 2017 corrobore cette hypothèse (voir la Figure 4 qui suit).
Identification des paramètres du modèle
Le système différentiel étant posé, il reste à identifier les paramètres inconnus du modèle. Ceux-ci sont au nombre de six :
- l’effet piston $\beta$ dont l’ordre de grandeur peut être déterminé par mesure ou simulation (voir nos travaux à ce sujet),
- le taux de renouvellement d’air par ventilation naturelle ou mécanique $\tau_0$,
- les termes source apparents $\alpha_a$, $\alpha_b$ qui donnent les proportions de particules fines et plus grosses émises par freinage et resuspension,
- les constantes de déposition $\delta_a$, $\delta_b$ qui sont en réalité identifiées à partir des diamètres d’aérosols équivalents $d_a,d_b$ : en effet, l’approche développée ici considère que la concentration totale en $PM_{10}$ est celle d’un aérosol composé de deux types de particules uniquement, en concentrations différentes.
L’identification fine de ces paramètres permet de retrouver assez fidèlement les concentrations mesurées en fonction du trafic ferroviaire, comme le montre la figure ci-dessous Figure 5, où l’on compare mesures et modèle.
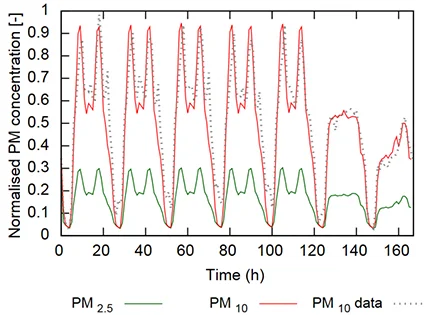
Les $PM_{2.5}$ sont également simulées par le modèle (voir courbe verte sur la Figure 5) mais sans confrontation expérimentale, ces mesures n’étant pas disponibles pour la gare de Saint-Michel lors de l’élaboration de ce document (ce paragraphe sera amené à être actualisé).
Le ratio $PM_{2.5}/PM_{10}$ obtenu, présenté en Figure 6, est toutefois très similaire à celui de la campagne expérimentale de [Fortain, 2007] (voir Figure 2).
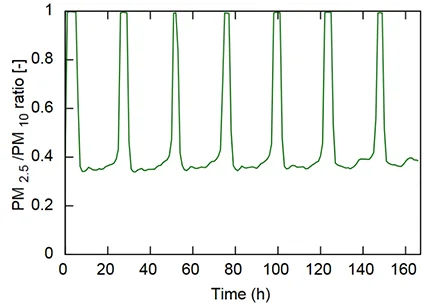
Dans l’attente de résultats expérimentaux, on juge que cette constatation conforte les résultats obtenus du modèle. Sur cette base, il est possible de simuler l’évolution de a concentration en PM10 en fonction de la ventilation et de la mise en place de filtration, en intégrant ces termes dans le modèle avec les paramètres identifiés.
Perspectives
Le modèle est en cours d’amélioration, au gré de la disponibilité des données mesurées. Deux axes majeurs sont en cours d’exploration : l’ajout de la quantité déposée sur les surfaces et la généralisation d’un modèle à $n$ classes.
Équation de fermeture
L’ajout de l’équation sur les surfaces ferme le système différentiel présenté auparavant omme dans [Qian et al. 2008] . On obtient ainsi :
$$ V \times \frac{\partial C}{\partial t} = a N + Q_{\text{v}} (C^{\text{ext}} - C) - \delta V C + \rho S_{\text{r}}L $$
$$ S_{\text{d}} \times \frac{dL}{dt} = \delta V C - \rho S_{\text{r}} L $$
Dans la première équation, $V$ est le volume de la gare, $Q_v$ est le débit d’air extérieur, $\delta$ est le taux de déposition, $\rho$ est la constante de resuspension, $S_r$ la surface accessible à la resuspension et $L$ la quantité de particules déposées par unité de surface [$\mu g/m^2$]. Dans la seconde équation, $S_d$ est la surface accessible à la déposition.
On notera que ces deux équations sont couplées par les termes croisés $\pm \delta V C$ et $\pm \rho S_r L$. Ceux-ci représentent respectivement la quantité de particules qui passe du “compartiment” d’air au “compartiment” de surface par déposition et la quantité remise en suspension depuis les surfaces vers le volume d’air.
Modèle à n classes
Avec un raisonnement similaire à celui utilisé pour deux classes de tailles de particules, il est possible d’étendre le modèle à nnn classes : ainsi on aurait la représentation de l’évolution d’un aérosol par classe de taille, comme présenté sur la figure qui suit.
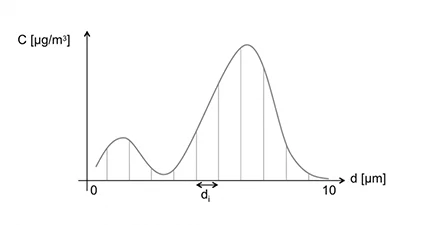
Il devient possible de définir les sources à partir de leur “spectre d’émission” par classe de taille. Un exemple est donné ci-dessous:

Parmis les verrous scientifiques à lever, on peut citer la quantité de particules initialement déposée, la différenciation du terme de resuspension par classe de taille (autrement dit : le “spectre de resuspension” pour lequel il n’existe pas encore de théorie unifiée) et enfin la confrontation expérimentale : les concentrations extérieures par classe de taille sont rarement disponibles et la quantité de particules déposées sur les surfaces est difficile à évaluer.