Ventilation naturelle en STD

Avec l’amélioration de la performance des enveloppes, les effets du vent sur la ventilation naturelle ont une part grandissante dans les consommations d’énergie. En simulation thermique dynamique, la modélisation de ces effets est très simplifiée par rapport à la réalité et peut être sensiblement améliorée par le recours à la simulation numérique.

Principe du calcul des débits de ventilation naturelle en STD

Pour illustrer le propos, on expose dans cette partie un cas simple de ventilation naturelle transversale liée aux effets du vent uniquement. Les outils actuels de STD déterminent le tirage transversal entre deux ouvrants \(a\) et \(b\) à une hauteur \(z\) en ayant recours à la théorie de Bernoulli  :

$$ Q_v = S_{\text{eq}} \times v(z) \times \sqrt{C_{\text{p}}^a − C_{\text{p}}^b} $$

où \(v(z)\) est la vitesse du vent à une hauteur \(z\) et \(C_{\text{p}}\) le coefficient de pression de chaque façade considérée. La surface équivalente \(S_{\text{eq}}\) est une moyenne pondérée des surfaces des ouvrants ainsi que de leurs coefficients de décharge, de sorte que :

$$ \frac{1}{S_{\text{eq}}^2} = \frac{1}{\left(C_{\text{d}}^a S_{a} \right)^2} + \frac{1}{\left(C_{\text{d}}^b S_{b} \right)^2} $$

où \(S_{a}\) et \(S_{b}\) représentent les surfaces respectives des ouvrants \(a\) et \(b\). Les coefficients de décharge \(C_{\text{d}}\)des mêmes ouvrants représentent deux phénomènes qui réduisent le débit théorique, Bernoulli faisant l’hypothèse que le fluide a une viscosité nulle. D’une part la veine se contracte après l’ouverture à cause des effets inertiels du jet et diminue le débit d’un coefficient \(C_{\text{c}}\) égal au rapport entre la surface de la veine après le passage de l’ouvrant et la surface de passage offerte (voir l’illustration Figure 1 pour deux formes simplifiées d’ouvrants). D’autre part les frottements visqueux atténuent le débit, ce qui est représenté par un facteur \(C_{\text{f}}\) généralement compris entre 0,95 et 0,99. Le coefficient de décharge est donc le produit \(C_{\text{d}} = C_{\text{c}} \times C_{\text{f}}\). La valeur couramment admise par le standard [ASHRAE, 1997]¹ et plusieurs logiciels de calcul de ventilation naturelle ( CONTAM , IES-VE MacroFlo , EnergyPlus ) est dans la plage allant de 0,60 à 0,65.

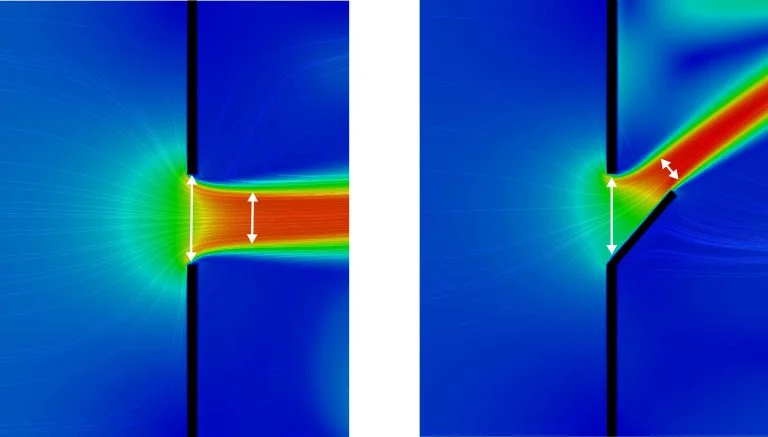
N’ayant pas d’accès direct à la pression de stagnation au niveau de l’ouvrant ni à la différence de pression entre les façades des ouvrants \(a\) et \(b\), on introduit un coefficient de pression \(C_{\text{p}}\) propre à chaque façade, qui représente une fraction de la pression dynamique “au loin” dans l’écoulement non perturbé, et peut être positif ou négatif en cas de surpression ou dépression :

$$ C_{\text{p}} = \frac{p_{\text{facade}}}{\frac{\rho \times v_{\text{ref}}^2}{2}} $$

où \(p_{\text{facade}}\) est la pression de stagnation sur la façade, \(\rho\) la masse volumique de l’air et \(v_{\text{ref}}\) la vitesse de référence.

Selon les logiciels, le coefficient \(C_{\text{p}}\) est déterminé de manière approchée en suivant des corrélations empiriques valides pour des géométries rectangulaires avec un facteur de forme proche de l’unité, incluant une correction en fonction de l’angle d’incidence du vent avec parfois une distinction pour les bâtiments de grande hauteur [Swami & Chandra, 1988]², [Akins, Peterka & Cermak, 1979]³.

La vitesse de l’écoulement non perturbé \(v_{\text{ref}}\) est prise égale à celle de la station météorologique la plus proche. Afin de déterminer la vitesse au niveau de l’ouvrant à la hauteur \(z\), on applique une loi atmosphérique telle que celle qui suit :

$$ v(z) = v_{\text{ref}} \times k_0 \times \ln\frac{z}{z_0} $$

Pour représenter l’environnement du bâtiment, le profil de cette équation de couche limite atmosphérique peut être modifié par les coefficients \(k_0\) et \(z_0\), respectivement la rugosité du site, comprise entre 0,14 et 0,25 et la longueur de rugosité, comprise entre 0,5 mm et 2 m, selon que le site est très ouvert (mer, champ de neige, désert sablonneux) ou très rugueux (centre des mégapoles, forêt tropicale).

Critique de la modélisation

La complexité des formes de bâtiment, leur implantation dans le tissu urbain ou la forme des ouvrants créent une réalité bien souvent éloignée de la théorie rappelée ci-dessus. Dans cette partie on s’attachera à montrer les écarts possibles sur les différents paramètres de la modélisation.

Coefficient de décharge

Le coefficient \(C_{\text{d}}\) est une grandeur en général mal documentée par les fabricants car elle varie en fonction de facteurs tels que le taux d’ouverture de l’ouvrant, la différence de température intérieur/extérieur, la vitesse d’air, comme recensé dans les travaux de recherche bibliographique de [Salliou, 2011]⁴ et ceux en préambule de la thèse de [Regard, 1996]⁵. De plus, ces derniers ont montré que la plage de variation s’étend de \(C_{\text{d}}\)=0,1 à \(C_{\text{d}}\)=2, influant donc de 10% à 200% sur la valeur du débit au travers de l’ouvrant. Il est cependant difficile de s’affranchir de cette incertitude sans une étude en soufflerie (numérique ou réelle). Selon les cas, il faudra donc adapter la valeur du \(C_{\text{d}}\) afin de se placer dans le cadre d’une hypothèse conservatrice et interpréter les résultats avec prudence.

Coefficient de pression

Ceux-ci sont très variables selon la direction du vent, sa vitesse locale en façade, la forme du bâtiment ainsi que la géométrie de son environnement proche et lointain. Sur une même façade d’un bâtiment à géométrie régulière, le \(C_{\text{p}}\) présente de plus des inhomogénéités importantes. La figure 2 montre un exemple de calcul du \(C_{\text{p}}\) en environnement urbain où la pression prend des valeurs disparates pouvant aller jusqu’à être positives et faiblement négatives en différents endroits d’une même paroi.

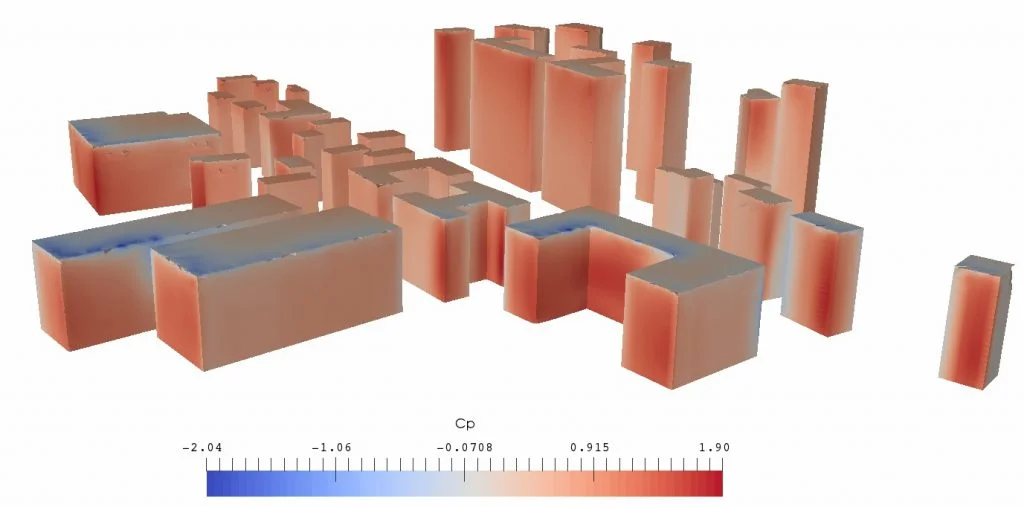
Vitesse d’air de référence

Elle est prise comme étant celle de la station météo dont on ne connaît pas la hauteur ni l’implantation. Il est donc difficile de conclure quant à la vitesse réelle aux abords du bâtiment, celle-ci dépendant de la topographie, de l’environnement urbain lointain et proche ainsi que des rugosités qui s’y rattachent. La figure 3, qui montre la complexité des écoulements en milieu urbain.

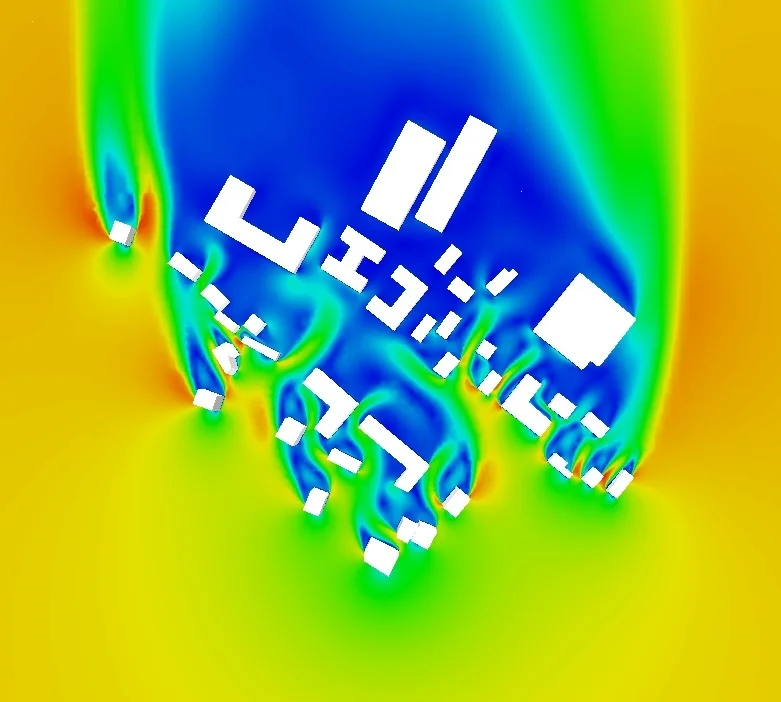
La réduction du nombre de paramètres incertains passe donc par la simulation aéraulique urbaine avec des logiciels libres ou disponibles dans le commerce qui résolvent les équations de Reynolds moyennées ainsi que la conservation de la masse (approche RANS) avec par exemple une modélisation de la turbulence de type \(k-\varepsilon\).

Cette approche permet de calculer explicitement le sur la façade en fonction de la rose des vents annuelle et de l’environnement urbain, réduisant ainsi l’incertitude sur les vitesses et la valeur des coefficients de pression. Les résultats de la simulation alimentent alors le calcul thermique dynamique annuel horaire. On notera que seuls les effets du vent sont considérés dans cette approche : le tirage thermique pourra être pris en compte par une condition sur le nombre de Richardson .